Digit Sum Discoveries

I've spent quite some time working with digit sums of numbers. My Odds 'n Evens recursive algorithm involved taking a number, adding to it the sum of its odd digits and subtracting the sum of its even digits. The number associated with my diurnal age today, 26658, is a member of OEIS A246420:

A246420

Numbers \(n\) such that (\(n\)+ digit sum of \(n\)) is a permutation of the decimal digits of \(n\).

In the case of 26658, the digit sum is 27 and adding to the number gives 26685. Such numbers account for about 0.923% of all the numbers between 1 and 26658 (permalink), or about 1 in every hundred. The initial members are:

0, 45, 234, 279, 423, 468, 612, 657, 801, 846, 1134, 1179, 1323, 1368, 1512, 1557, 1701, 1746, 1890, 1935, 2034, 2079, 2223, 2268, 2412, 2457, 2601, 2646, 2835, 3123, 3168, 3312, 3357, 3501, 3546, 3735, 3924, 3969, 4023, 4068, 4212, 4257, 4401, 4446, 4635, 4824, 4869, 5112, 5157, 5301 

I was prompted to investigate the following question: do all numbers eventually become permutations of their original digits if the process of adding the sum of digits of a number to the number is carried out repeatedly. I initially looked at 26658's neighbour, 26659. It turns out that a permutation is reached after 12 cycles and the trajectory is:

26659, 26687, 26716, 26738, 26764, 26789, 26821, 26840, 26860, 26882, 26908, 26933, 26956

However, that's not the end of the story because permutations are also reached after 1566 and 1848 cycles leading to 59266 and 65269 respectively. Clearly some permutations are not attainable because they are less than 26659 but most are larger and are not attained. Once the sum exceeds 99999, no further permutations are possible of course.

What about 26658's smaller neighbour 26657? The first permutation is reached after 42 cycles and the trajectory is:

26657, 26683, 26708, 26731, 26750, 26770, 26792, 26818, 26843, 26866, 26894, 26923, 26945, 26971, 26996, 27028, 27047, 27067, 27089, 27115, 27131, 27145, 27164, 27184, 27206, 27223, 27239, 27262, 27281, 27301, 27314, 27331, 27347, 27370, 27389, 27418, 27440, 27457, 27482, 27505, 27524, 27544, 27566.

Once again, other permutations are reached. Here is the full list:

• 26657 leads to the permutation 27566 after 42 cycles
• 26657 leads to the permutation 57266 after 1488 cycles
• 26657 leads to the permutation 62675 after 1728 cycles
• 26657 leads to the permutation 66725 after 1902 cycles
• 26657 leads to the permutation 75266 after 2262 cycles

Once we try 26656 however, we find that no permutations are reached. Further investigation shows that most number in the vicinity of 26658 do reach a permutation, partly because most permutations are larger. As we approach 99999 of course, this likelihood diminishes. Getting back to 26658, we discover that it reaches far more than the normal number of permutations. Here is the full list (permalink):

• 26658 leads to the permutation 26685 after 1 cycles
• 26658 leads to the permutation 26865 after 9 cycles
• 26658 leads to the permutation 28566 after 86 cycles
• 26658 leads to the permutation 28665 after 90 cycles
• 26658 leads to the permutation 52686 after 1272 cycles
• 26658 leads to the permutation 52866 after 1280 cycles
• 26658 leads to the permutation 56286 after 1434 cycles
• 26658 leads to the permutation 56862 after 1457 cycles
• 26658 leads to the permutation 58266 after 1513 cycles
• 26658 leads to the permutation 58662 after 1528 cycles
• 26658 leads to the permutation 62586 after 1707 cycles
• 26658 leads to the permutation 62865 after 1719 cycles
• 26658 leads to the permutation 65286 after 1826 cycles
• 26658 leads to the permutation 65862 after 1849 cycles
• 26658 leads to the permutation 66825 after 1887 cycles
• 26658 leads to the permutation 66852 after 1888 cycles
• 26658 leads to the permutation 68265 after 1942 cycles
• 26658 leads to the permutation 68562 after 1953 cycles
• 26658 leads to the permutation 68625 after 1955 cycles
• 26658 leads to the permutation 68652 after 1956 cycles
• 26658 leads to the permutation 82566 after 2530 cycles
• 26658 leads to the permutation 82665 after 2534 cycles
• 26658 leads to the permutation 85266 after 2639 cycles
• 26658 leads to the permutation 85662 after 2654 cycles
• 26658 leads to the permutation 86265 after 2676 cycles
• 26658 leads to the permutation 86562 after 2687 cycles
• 26658 leads to the permutation 86625 after 2689 cycles
• 26658 leads to the permutation 86652 after 2690 cycles

Is this a record for five digit numbers? It would an interesting question to explore. Five distinct digits can be arranged to form a number in factorial 5 or 120 different ways. With repeated digits the number of permutations will be smaller. For example, 26658 achieves 28 out of a possible 57. There are 60 permutations altogether but the three smaller permutations (25668, 25686 and 25866) are not attainable. 

How frequent are numbers like 26656 that do not reach a permutation? Well, in the range between 26500 and 26700, there are 25 such numbers, representing 12.5%. The numbers are (permalink):

26522, 26525, 26533, 26552, 26555, 26566, 26602, 26606, 26611, 26620, 26623, 26626, 26627, 26632, 26638, 26656, 26660, 26662, 26665, 26672, 26678, 26683, 26687, 26696, 26698

Such percentages are quite variable. For example, in the range of 200 numbers from 9799 to 9999, 193 of or 96.5% of the numbers do not reach a permutation. This is because the range is close to the four digit cutoff. 

Obviously this is a topic that can be explored in far more depth but this post is a start and I'll probably follow up with further posts as I find out more.

ADDENDUM: August 18th 2023

It's interesting to look at the records for numbers of cycles taken to reach a permutation using the number + sum of digits of number recursively. Up to 100,000 the records are as follows (permalink with limit set at 100,000):

12 leads to the permutation 21 after 2 cycles

15 leads to the permutation 51 after 6 cycles

18 leads to the permutation 81 after 7 cycles

108 leads to the permutation 180 after 8 cycles

123 leads to the permutation 213 after 10 cycles

125 leads to the permutation 251 after 12 cycles

134 leads to the permutation 341 after 18 cycles

144 leads to the permutation 414 after 25 cycles

152 leads to the permutation 521 after 30 cycles

156 leads to the permutation 561 after 34 cycles

158 leads to the permutation 851 after 48 cycles

180 leads to the permutation 801 after 50 cycles

189 leads to the permutation 819 after 51 cycles

1012 leads to the permutation 2011 after 72 cycles

1027 leads to the permutation 2107 after 78 cycles

1034 leads to the permutation 3041 after 132 cycles

1037 leads to the permutation 7031 after 366 cycles

1079 leads to the permutation 9017 after 462 cycles

10005 leads to the permutation 50001 after 2002 cycles

10027 leads to the permutation 70102 after 2964 cycles

10069 leads to the permutation 90061 after 3762 cycles

10229 leads to the permutation 92120 after 3840 cycles

11199 leads to the permutation 99111 after 3900 cycles

100020 leads to the permutation 200100 after 4384 cycles

100033 leads to the permutation 300031 after 8802 cycles

100067 leads to the permutation 601070 after 20640 cycles

100117 leads to the permutation 700111 after 24198 cycles

100177 leads to the permutation 770110 after 26742 cycles

100309 leads to the permutation 900301 after 31026 cycles

100399 leads to the permutation 991030 after 33990 cycles

As can be seen, up to 100,000 the record of 3900 cycles is held by 11199 that eventually reaches the permutation 99111 that is the reversal of the original number. Up to one million, the record of 33990 cycles is held by 100399 that reaches the permutation 991030.

Dream Numbers

This post is a little different from my usual content that is often prompted by an analysis of the number associated with my diurnal age. This post is prompted by a dream that I had involving a shipping container that, unlike most such containers, was gun metal in colour. It seemed totally sealed but I found a tiny opening and lit a match (or used the torch on my phone) to peer within. I saw a woman peering back at me.

She invited me in and the front face of the container disappeared so that access was now possible. She said that there were 37 people inside. Two of those were adolescent boys, one noticeably shorter than the other. It seemed that one of them was 17 but I wasn't sure which one. I pointed to the taller boy and then, quite audibly in my dream, said "seventeen?". The woman, and the mother of the two boys, smiled and clarified the situation. She said that they were twins (clearly not identical) and had been born on a Saturday. They were both 17.

After some thinking about these numbers, I realised that both 17 and 37 are 4\(k\)+1 primes and thus form the hypotenuse of right angled triangles with associated integer sides, connected by Pythagoras' Theorem:$$ \begin{align} 17^2&=8^2+15^2\\37^2&=12^2+35^2 \end{align}$$Thus we end up with a set of six numbers:$$8, 12, 15, 17, 35, 37$$Being 4\( k\)+1 primes of course, we can also write:$$ \begin{align} 17&=1^2+4^2\\37&=1^2+6^2 \end{align}$$This generates a set of five numbers:$$1, 4, 6, 17, 37$$I tend to go with the set of six numbers as they are easily associated with the Saturday night draw in the Australian lottery system. 

Being in Indonesia, I can't participate in this lottery, not even using a VPN, so I passed these numbers on to my daughter-in-law who lives in Melbourne. I suggested that she try them out. Whether she does or doesn't, I'll report back on what numbers came up in the Saturday night draw at the end of this post. I won't make the post public until after Saturday night in case anyone tries to "cash in" on my dream numbers!

LATE SATURDAY NIGHT

Well my daughter-in-law did submit the six numbers and, not surprisingly, my dream numbers did not prove precognitive. In fact I only succeeded in selecting one of the winning numbers and therefore not even a minor prize was won. See Figure 1. Nor did my other possible numbers (1, 4 and 6) make an appearance. Of course, the numbers could have been meant for Saturday April 2nd, the day before my birthday and a day that marks the 73rd solar return (when the Sun returns to the exact position that it occupied at the time of my birth).

Figure 1

Here are links to my two previous posts on the mathematics of Lotto:

• Lotto Simulations on October 20th 2018
• Lotto Loser on June 10th 2019

Of course the numbers 17 and 37 that I dreamed of may have had nothing to do with Lotto. In fact, Figure 2 gives an insight into a completely different interpretation of the numbers.

Figure 2

A shipping container is characterised by its square cross-section and so the 17 could refer to the side of this square and the 37 could refer to its length of the prism. Only two numbers are needed to define its dimensions.  When the front of the container is open and you look at it front on, the far end seems to be smaller than the open front end.  This corresponds to the twins being both 17 and yet one appearing larger than the other. 

What are the characteristics of this 17 x 17 x 37 rectangular prism? It has a volume of 10693 cubic units and a surface area of 3094 square units. If the front end is open, then the surface area is 2805 square units. How Saturday fits in with this view of things I don't know. Saturday is the sixth day of the week if we count Monday as 1, Tuesday as 2 etc. A rectangular prism does indeed have six sides.

Saturday is Saturn's day and each planet has an associated magic square. The one for Saturn is shown in Figure 3. The numbers associated with Saturn are 3, 9, 15 and 45 because the magic square is 3 x 3, there are 9 squares, the numbers in each row, column and main diagonal add to 15 and the total of all nine numbers is 45.

Figure 3

I've written about magic squares before. Here are links to these posts:

• Ultramagic Squares on November 12th 2021
• Prime Semi-Magic Squares on May 17th 2021
• Magic Squares on September 21st 2020
• Anti-Magic Squares on July 17th 2018

Other sources quote Saturn as being associated with the number 8. See Figure 4.

Figure 4: source

I seem to be going off on a tangent here so I'll stop. It has occurred to me that 17 and 37 are both reversible primes since 71 and 73 are also prime. Currently, at age 72, I'm stuck between these two primes although in less than two weeks I'll be 73. 

Let's not forget that 71 and 73 are also twin primes which fits in very nicely with the twin element in the dream. Additionally, my 73rd solar return occurs on April 2nd 2022, a Saturday. The solar return marks the return of the Sun to the same zodiacal position (12°47'07" Aries) at the time of my birth. My birthday actually occurs on April 3rd.

The shipping container may just be a symbolic representation of life on the physical plane. I am reminded of Carl Jung's description of his Near Death Experience in his autobiography "Memories, Dreams, Reflections" :

In reality, a good three weeks were still to pass before I could truly make up my mind to live again. I could not eat because all food repelled me. The view of city and mountains from my sick-bed seemed to me like a painted curtain with black holes in it, or a tattered sheet of newspaper full of photographs that meant nothing. Disappointed, I thought, "Now I must return to the 'box system' again." For it seemed to me as if behind the horizon of the cosmos a three-dimensional world had been artificially built up, in which each person sat by himself in a little box. And now I should have to convince myself all over again that this was important! Life and the whole world struck me as a prison, and it bothered me beyond measure that I should again be finding all that quite in order. I had been so glad to shed it all, and now it had come about that I along with everyone else would again be hung up in a box by a thread.

He continued:

It is impossible to convey the beauty and intensity of emotion during those visions. They were the most tremendous things I have ever experienced. And what a contrast the day was: I was tormented and on edge; everything irritated me; everything was too material, too crude and clumsy, terribly limited both spatially and spiritually. It was all an imprisonment, for reasons impossible to divine, and yet it had a kind of hypnotic power, a cogency, as if it were reality itself, for all that I had clearly perceived its emptiness. Although my belief in the world returned to returned to me, I have never since entirely freed myself of the impression that this life is a segment of existence which is enacted in a three-dimensional boxlike universe especially set up for it.

So perhaps my dream primes 17 and 37 are meant to be interpreted as the twin primes 71 and 73 with Saturday April 2nd marking my astrological coming of age 73. I realise I'm straying too far into the metaphysical here and it would be better to continue this train of thought in my blog "Mystical Meanderings".

Odds 'n Evens Visualisation

I've written about the behaviour of numbers under the repeated application of the odds and evens rule in numerous posts but I'll recapitulate the rule here:

• start with an number
• any even digits are given a negative face value
• any odd digits are given a positive face value
• find the sum of the face value of the digits
• add this sum to the number to generate a new number
• repeat the process until a fixed value or a loop is reached

As an example, consider the number 111. Under the above rules we have, 111 --> 111+3 --> 114-2 --> 112 and a fixed value has been reached because 112 is invariant under the rule. Take 13 as an another example. The progression here is 13 --> 13+4 --> 17+8 --> 25+3 --> 28-10 --> 18-7 --> 11+2--> 13 and we are back where we started.

What I've attempted to do in Figure 1 is to show the behaviour of the numbers from 1 to 256 by inserting them into a 16 x 16 grid. I'll now explain the significance of the colours used.

Figure 2

Referring to Figure 2 : 1, 2, 3, 4, 6 and 8 are in white squares. These numbers all reach zero in one or two iterations. Thus for them 0 is the fixed point, although it is not marked on the grid. 5, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 21, 22, 23, 24, 25, 26 and 28 are all coloured the same but some numbers are bold and noticeably larger. These numbers (11, 13, 17, 18, 25 and 28) form a loop and the other numbers (smaller and not bold) will end up in this loop after repeated applications of the odds 'n evens rule. I've chosen the term vortices (plural of vortex) for such loops and vorticals for the numbers that comprise them. The numbers that fall into the loop are captives.

********************************************************************************

Figure 3

Referring to Figure 3 : the next numbers are in blue coloured squares and are clearly the most numerous. There is only one number that is bold and larger than the others. That number is 134 and it is invariant under the rule. All the other blue numbers have trajectories that lead to 134. I've chosen to call numbers like 134 attractors and the numbers that lead to them I've called captives.

********************************************************************************

Figure 4

Referring to Figure 4 : the next loop is made up of the numbers 54, 55, 64 and 65 and all the other similarly coloured numbers will end up in this loop or vortex.

********************************************************************************

Figure 5

Referring to Figure 5 : 112 is a number that is invariant under the rule and all the other similarly coloured numbers have trajectories that lead to 112. Having the same digits as 112 is 121 and so this too is a number that is also invariant under the rule. It has been made bold and larger but its square is left white because no other numbers have trajectories that lead to it. Similarly, 143, 156, 165, 187 and 211 are singletons and have no connections to the numbers around them. In the past I've called such numbers attractors, even though no other numbers are attracted to them. The preferable term might be isolates.

********************************************************************************

Figure 6

Referring to Figure 6 : 137 and 148 are larger and bold because they form a loop and the other similarly coloured numbers will all end up in this loop or vortex. These two number loops as we will see are fairly common.

********************************************************************************

Figure 7

Referring to Figure 7 : 155 and 166 similarly form a loop or vortex and all the other grey coloured numbers will enter this loop.

********************************************************************************

Figure 8

Referring to Figure 8 : 156 is invariant under the rule and all yellow coloured numbers have trajectories leading to 156. I've chosen the term attractor to describe numbers such as 156.

********************************************************************************

Figure 9

Referring to Figure 9 : 173 and 184 form a loop or vortex and the other brown coloured numbers will end up in this loop. 178 is invariant under the rule and other red coloured numbers have trajectories leading to 178. I've chosen to use the term attractor for numbers like 178.

********************************************************************************

Figure 10

Referring to Figure 10 : 198 and 200 form a loop and the other pink coloured numbers will end up in this loop or vortex.

********************************************************************************

Figure 11

Referring to Figure 11 : 209 and 216 form a loop and the other green coloured numbers will end up in this loop or vortex.

********************************************************************************

Figure 12

Referring to Figure 12 : 231, 233, 237, 245, 244 and 234 form a loop or vortex into which all the other similarly coloured numbers will end up. 239 and 249 to 256 have trajectories leading to a loop that is beyond the grid so they have been made grey.

The intention of this visualisation was to provide an overview of the behaviour of the first 256 counting numbers under the odds 'n evens rule. As can be clearly seen the numbers fall into various categories:

• attractors: these are numbers that are invariant under the odds 'n evens rule and the trajectories of one or more other numbers (called captives) lead to them e.g. 112. This number has a total of nine captives: 93, 97, 105, 110, 111, 113, 114, 116, 118.
  
  
• isolates: this is a new term that I've introduced to describe numbers that are invariant under the odds 'n evens rule but have no captives e.g. 121.
  
  
• vorticals: this is a made-up word that I've used to describe numbers that form part of a vortex or loop. The trajectories of some other numbers, called captives, will end up in this vortex e.g. 209 is a vortical forming part of the vortex {209, 216}. The numbers 195, 197, 199, 207, 210, 212, 214, 215, 217, 218, 220, 221, 222, 223, 224, 225, 226, 228 are all captives of this vortex.
  
  
• captives: these numbers have trajectories that lead either to an attractor or a vortex e.g. 113 is a captive of the attractor 112 while 224 is a captive of the vortex {209, 216}.

Below are some links to earlier posts relating to the odds 'n evens rule:

• Odds and Evens on June 17th 2021
• Attractors, Vortices and Captives on June 18th 2021
• Binary Odds and Evens on June 19th 2021
• Odds and Evens: Statistics on June 21st 2021
• Kaprekar's Routine on July 16th 2021
• The Modest Magnetism of 26596 on January 22nd 2022
• Higher Order Odds and Evens Trajectory on March 12th 2022
• Second Order Odds and Evens Trajectory for Numbers 1 to 99 on March 12th 2022
• Third Order Odds and Evens Trajectory for Numbers 1 to 10 on March 12th 2022

Doublets, Triplets etc.

One of the many properties associated with my diurnal age today of 26553 is that it's a member of OEIS A116057: 

A116057

\(n\) times \( \Pi(n) \) is made of nontrivial runs of identical digits, where \( \Pi(n) \) is the prime counting function that returns the number of primes less than or equal to a given number.

It took me a little thought to get an algorithm that would return the members of this sequence but eventually I succeeded. While it may not be the most elegant of algorithms, it does get the job done. I've embedded the code from SageMathCell (permalink) below:

As can be seen the initial members of the sequence, up to 40,000, are:

[11, 37, 66, 154, 332, 750, 1696, 4000, 13684, 22308, 26640, 26653, 30327]

Taking the last member of the sequence, it can be seen that:$$ 30377 \times { \Large \Pi } (30327) =99442233 $$The algorithm is easily modifiable and below it is used to generate the initial terms of OEIS A033023:

A033023

Numbers whose base-10 expansion has no run of digits with length < 2.

Here the members of sequence, up to 40,000, are:

[11, 22, 33, 44, 55, 66, 77, 88, 99, 111, 222, 333, 444, 555, 666, 777, 888, 999, 1100, 1111, 1122, 1133, 1144, 1155, 1166, 1177, 1188, 1199, 2200, 2211, 2222, 2233, 2244, 2255, 2266, 2277, 2288, 2299, 3300, 3311, 3322, 3333, 3344, 3355, 3366, 3377, 3388, 3399, 4400, 4411, 4422, 4433, 4444, 4455, 4466, 4477, 4488, 4499, 5500, 5511, 5522, 5533, 5544, 5555, 5566, 5577, 5588, 5599, 6600, 6611, 6622, 6633, 6644, 6655, 6666, 6677, 6688, 6699, 7700, 7711, 7722, 7733, 7744, 7755, 7766, 7777, 7788, 7799, 8800, 8811, 8822, 8833, 8844, 8855, 8866, 8877, 8888, 8899, 9900, 9911, 9922, 9933, 9944, 9955, 9966, 9977, 9988, 9999, 11000, 11100, 11111, 11122, 11133, 11144, 11155, 11166, 11177, 11188, 11199, 11222, 11333, 11444, 11555, 11666, 11777, 11888, 11999, 22000, 22111, 22200, 22211, 22222, 22233, 22244, 22255, 22266, 22277, 22288, 22299, 22333, 22444, 22555, 22666, 22777, 22888, 22999, 33000, 33111, 33222, 33300, 33311, 33322, 33333, 33344, 33355, 33366, 33377, 33388, 33399, 33444, 33555, 33666, 33777, 33888, 33999]

Of course, the algorithm is easily modifiable to find numbers whose base-\(n\) expansion has no run of digits with length < 2. Here \(n \) can range from 2 to 36. For example, if \(n\)=16, then the numbers up to 40,000 that satisfy are:

[17, 34, 51, 68, 85, 102, 119, 136, 153, 170, 187, 204, 221, 238, 255, 273, 546, 819, 1092, 1365, 1638, 1911, 2184, 2457, 2730, 3003, 3276, 3549, 3822, 4095, 4352, 4369, 4386, 4403, 4420, 4437, 4454, 4471, 4488, 4505, 4522, 4539, 4556, 4573, 4590, 4607, 8704, 8721, 8738, 8755, 8772, 8789, 8806, 8823, 8840, 8857, 8874, 8891, 8908, 8925, 8942, 8959, 13056, 13073, 13090, 13107, 13124, 13141, 13158, 13175, 13192, 13209, 13226, 13243, 13260, 13277, 13294, 13311, 17408, 17425, 17442, 17459, 17476, 17493, 17510, 17527, 17544, 17561, 17578, 17595, 17612, 17629, 17646, 17663, 21760, 21777, 21794, 21811, 21828, 21845, 21862, 21879, 21896, 21913, 21930, 21947, 21964, 21981, 21998, 22015, 26112, 26129, 26146, 26163, 26180, 26197, 26214, 26231, 26248, 26265, 26282, 26299, 26316, 26333, 26350, 26367, 30464, 30481, 30498, 30515, 30532, 30549, 30566, 30583, 30600, 30617, 30634, 30651, 30668, 30685, 30702, 30719, 34816, 34833, 34850, 34867, 34884, 34901, 34918, 34935, 34952, 34969, 34986, 35003, 35020, 35037, 35054, 35071, 39168, 39185, 39202, 39219, 39236, 39253, 39270, 39287, 39304, 39321, 39338, 39355, 39372, 39389, 39406, 39423]

In the OEIS, this is sequence A033029:

A033029

Numbers whose base-16 expansion has no run of digits with length < 2.

Here is a permalink to the algorithm. For example, take 26316 from this list as an example. We have \(26316_{{\small 10}}=66\text{cc}_{ {\small 16}}\).

The algorithm can be used to find some numbers with interesting properties. For example, in the range up to one million, what members of OEIS A033023 (sequence listed earlier) have a totient that is also a member of OEIS A033023? I won't embed the code but here is a permalink to the algorithm that I used to find the numbers with the required property. It turns out that there are only three:

• \( \phi(9922)=4400\)
• \( \phi(662233)=554400\)
• \( \phi(990022)=449900\)

Base-a Wieferich Primes

Before delving into what base-\(a\) Wieferich primes are, we need to be clear about what is meant by Wieferich prime. Interestingly, only two are known.  Here is a quote from Wikipedia:

In number theory, a Wieferich prime is a prime number \(p\) such that \(p^2\) divides \(2^{p − 1} − 1\), therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides \(2^{p − 1}− 1\). Wieferich primes were first described by Arthur Wieferich in 1909 in works pertaining to Fermat's Last Theorem, at which time both of Fermat's theorems were already well known to mathematicians.

Since then, connections between Wieferich primes and various other topics in mathematics have been discovered, including other types of numbers and primes, such as Mersenne and Fermat numbers, specific types of pseudoprimes and some types of numbers generalized from the original definition of a Wieferich prime. Over time, those connections discovered have extended to cover more properties of certain prime numbers as well as more general subjects such as number fields and the \(abc\) conjecture.

As of March 2021, the only known Wieferich primes are 1093 and 3511 (sequence A001220 in the OEIS).

If we relax the condition that the base has to be 2 then we open the door to what are called base-\(a\) Wieferich primes. Let's make \(a=3\) and ask the question what primes satisfy:$$3^{p-1} \equiv 1 \pmod{p^2} \text{ or } 3^{p-1} -1\equiv 0 \pmod{p^2}$$A little testing will show that the smallest value of \(p\) to satisfy this condition is 11. The next prime to satisfy is 1006003 and no prime has been found beyond that as yet.

OEIS A039951 records the smallest solutions for \(a^{p-1} \equiv 1 \pmod{p^2} \) for various values of \(a\). The first 46 values are:

2, 1093, 11, 1093, 2, 66161, 5, 3, 2, 3, 71, 2693, 2, 29, 29131, 1093, 2, 5, 3, 281, 2, 13, 13, 5, 2, 3, 11, 3, 2, 7, 7, 5, 2, 46145917691, 3, 66161, 2, 17, 8039, 11, 2, 23, 5, 3, 2, 3

No primes have been found that satisfy 47, 72, 186, 187, 200, 203, 222, 231, 304, 311, 335, 355, 435, 454, 546, 554, 610, 639, 662, 760, 772, 798, 808, 812, 858, 860, 871, 983, 986, ...  although it is conjectured that there are infinitely many solutions for every \(a\). Table 1 shows Wieferich primes for various values of \(a\):

Table 1: source

I came across these primes when researching properties associated with my diurnal age of 26645.  It turns out that this number is a member of OEIS A344827:

A344827

\(s_n\) is the smallest \(a \gt 1\) such that prime(\(n\)), prime(\(n\)+1) and prime(\(n\)+2) are all base-\(a\) Wieferich primes.

The members of the sequence from \(n=1 \dots 8\) are 449, 226, 1207, 606, 3469, 653, 5649 and 26645. Now prime(8)=19 and thus we have 26645 as the smallest value of \(a\). Thus we have:$$26645^{19-1} \equiv 1 \pmod{19^2} \\26645^{23 -1} \equiv 1 \pmod{23^2} \\26645^{29-1}  \equiv 1 \pmod{29^2}$$

Truncatable Primes

I've not dedicated a post to truncatable primes since I started this blog in 2015 but I was prompted to do so because one of the properties associated with my diurnal age today, 26644, is that it's a member of OEIS A346662:

A346662

Number of \(n\)-digit left- or right-truncatable primes with no consecutive zero digits.

The number of members of this sequence is finite and consists of:

4, 16, 76, 300, 955, 2648, 6402, 14339, 28684, 53450, 91284, 147064, 221301, 319067, 433227, 567565, 700765, 834464, 947055, 1050886, 1114368, 1157526, 1150645, 1117265, 1044757, 963722, 855804, 753172, 633786, 528122, 426328, 339866, 264078, 202013, 150330, 111055, 78996, 56123, 38874, 26644, 17944, 11898, 7878, 4945, 3255, 2024, 1323, 764, 464, 286, 158, 77, 40, 26, 14, 5, 5, 4, 1, 1

The sequence member 26644 corresponds to \(n\)=40. Thus there are 26644 40-digit primes that are left-or right-truncatable. The reason for having no consecutive zero digits is that, without this restriction, suitable primes could be made indefinitely long. The comments to the OEIS entry are as follows:

A left- or right-truncatable prime is a prime number from which one digit at a time may be removed from the left or right end until a single-digit prime is reached, with each digit removal resulting in a prime. There exists only one such 60-digit prime: 

202075909708030901050930450609080660821035604908735717137397 

Since it cannot be extended, there are no such primes with more than 60 digits, so a(60)=1 is the final term of the sequence.

The OEIS sequence listing these primes is A347864:

A347864

Left-or right-truncatable primes, restricted to one consecutive zero.

The sequence begins as follows:

2, 3, 5, 7, 13, 17, 23, 29, 31, 37, 43, 47, 53, 59, 67, 71, 73, 79, 83, 97, 103, 107, 113, 131, 137, 139, 167, 173, 179, 197, 223, 229, 233, 239, 271, 283, 293, 307, 311, 313, 317, 331, 337, 347, 353, 359, 367, 373, 379, 383, 397, 431, 433, 439, 443, 467, 479, 503 

The OEIS comments state that:

There are 16,484,138 primes in this list, in total. The largest one has 60 digits and there is only one of that length.

Generally however, when considering truncatable primes, zeros are not allowed at all. One such OEIS sequence with this restriction is OEIS A137812:

A137812

Left- or right-truncatable primes.

This finite sequence begins as follows:

2, 3, 5, 7, 13, 17, 23, 29, 31, 37, 43, 47, 53, 59, 67, 71, 73, 79, 83, 97, 113, 131, 137, 139, 167, 173, 179, 197, 223, 229, 233, 239, 271, 283, 293, 311, 313, 317, 331, 337, 347, 353, 359, 367, 373, 379, 383, 397, 431, 433, 439, 443, 467, 479, 523, 547, 571, ...

For example, 313 --> 13 --> 3 or 313 --> 31 --> 3. Another example is 443 --> 43 --> 3. Note that this sequence lists the actual primes and not the number of possible \(n\)-digit primes. The OEIS comments state that:

Repeatedly removing a digit from either the left or right produces only primes. There are 149,677 terms in this sequence, ending with a 31 digit prime: 

8939662423123592347173339993799

In the previous process, we have the option of successively moving one digit from the left OR right but different constraints can be imposed. Three of these are:

1. digits can only be removed from the left (this produces the left-truncatable primes)
2. digits can only be removed from the right (this produces the right-truncatable primes)
3. digits must be removed in pairs (one from the left and one from the right, simultaneously)

The left-truncatable primes comprise OEIS  A024785: 

A024785

Left-truncatable primes: every suffix is prime and no digits are zero.

An example is 1223 because 1223, 223, 23 and 3 are all prime. There are 4620 such primes, the largest being 357686312646216567629137. The sequence begins:

2, 3, 5, 7, 13, 17, 23, 37, 43, 47, 53, 67, 73, 83, 97, 113, 137, 167, 173, 197, 223, 283, 313, 317, 337, 347, 353, 367, 373, 383, 397, 443, 467, 523, 547, 613, 617, 643, 647, 653, 673, 683, 743, 773, 797, 823, 853, 883, 937, 947, 953, 967, 983, 997, 1223, ...

The right-truncatable primes comprise OEIS A024770:

A024770

Right-truncatable primes: every prefix is prime.

An example is 31193 because 31193, 3119, 311, 31 and 3 are all prime. There are 83 such primes, the largest being 73939133. The sequence begins:

2, 3, 5, 7, 23, 29, 31, 37, 53, 59, 71, 73, 79, 233, 239, 293, 311, 313, 317, 373, 379, 593, 599, 719, 733, 739, 797, 2333, 2339, 2393, 2399, 2939, 3119, 3137, 3733, 3739, 3793, 3797, 5939, 7193, 7331, 7333, 7393, 23333, 23339, 23399, 23993, 29399, 31193, ...

There are 15 primes that are both left- and right-truncatable and form OEIS A020994:

2, 3, 5, 7, 23, 37, 53, 73, 313, 317, 373, 797, 3137, 3797, 739397

The bi-truncatable primes comprise OEIS A077390:

A077390

Primes which leave primes at every step if most significant digit and least significant digit are deleted until a one digit or two digit prime is obtained.

An example is 21313 because 21313, 131 and 3 all are primes. The sequence begins:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 127, 131, 137, 139, 151, 157, 173, 179, 223, 227, 229, 233, 239, 251, 257, 271, 277, 331, 337, 353, 359, 373, 379, 421, 431, 433, 439, 457, 479, 521, 523, 557, 571, 577, 631, 653, 659, ...

The OEIS comments state that:

There are exactly 920,720,315 such primes, the largest being 9161759674286961988443272139114537477768682563429152377117139 1111313737919133977331737137933773713713973.

There are exactly 331,780,864 odd length primes and 588,939,451 even length primes, the largest odd length prime being

7228828176786792552781668926755667258635743361825711373791931117197999133917737137399993737111177

Third Order Odds and Evens Trajectory for Numbers 1 to 10.

My previous post was titled Second Order Odds and Evens Trajectory for Numbers 1 to 99 and in this post I will be looking at the behaviour of the numbers from 1 to 10 under the recursive rule:

number --> number + \( \sum d_o^3 - \sum d_e^3 \) 

where \( d_o^3 \) are the number's odd digits raised to the power \( 3\) and \( d_e^3 \) are the number's even digits raised to the power \( 3\).  There is more variability with the numbers when \(k=3\) so I'm restricting my analysis to just the numbers from 1 to 10. A full analysis from 1 to 99 would be too lengthy but this is the beginning of the third order analysis and I'll follow up with more numbers in a future post.

Figure 1 shows the trajectory for the number 1. The entire trajectory consists of 161 steps and begins with 1, 2, -6, 210, 203, 222, 198, ... . The numbers that are in the final loop are {-7721, -8400, -7824, -7583, -7566, -7602}. The minimum value reached is -8441.

Figure 1

Here we see how the power of 3 drives the trajectory into increasingly negative territory until there is a brief rally after which the loop is reached.

 

2 is on exactly the same trajectory as 1 since 1 --> 2 under the odds and evens rule.

3 has a brief trajectory of only 14 steps: 3, 30, 57, 525, 767, 1237, 1600, 1385, 1026, 803, 318, -166, 265, 166, -265, -166 and ends in the loop {-166, 265, 166, -265}. See Figure 2.

Figure 2

30 and 57 also lie on the path of 3 and thus end in the same {-166, 265, 166, -265} loop.

4 follows a similar pattern to 1 and 2 except that the maximum value is +8441 and the loop is the same except that the members are positive {7721, 8400, 7824, 7583, 7566, 7602}. See Figure 3.

Figure 3

5 and 6 and 7 have lengthy trajectories but eventually end up in the same positive loop as 4.

8 produces a new trajectory that plummets to a record low of -34870 and ends in the loop {-34203, -34185, -33762, -33935, -34870, -34664, -34131, -34123, -34106, -33854, -33457, -33915, -34824} after 169 steps. See Figure 4.

Figure 4

9 follows a similar trajectory to 1 and 2 ending in the negative loop {-7721, -8400, -7824, -7583, -7566, -7602}.

10 follows a similar trajectory to 4, 5, 6 and 7 ending in the positive loop {7721, 8400, 7824, 7583, 7566, 7602}. 

So in summary:

• 1, 2 and 9 end in the loop {-7721, -8400, -7824, -7583, -7566, -7602}.
• 3 ends in the loop {-166, 265, 166, -265}.
• 4, 5, 6, 7 and 10 end in the loop {7721, 8400, 7824, 7583, 7566, 7602}. 
• 8 ends in the loop {-34203, -34185, -33762, -33935, -34870, -34664, -34131, -34123, -34106, -33854, -33457, -33915, -34824}.

Second Order Odds and Evens Trajectory for Numbers 1 to 99

In my previous post titled Higher Order Odds and Evens Trajectory, I looked specifically at the trajectory of the number 26638 under the recursive rule that:

number --> number + \( \sum d_o^k - \sum d_e^k \) with \(k \geq 1\)

where \( d_o^k \) are the number's odd digits raised to the power \( k\) and \( d_e^k \) are the number's even digits raised to the power \( k\).  In that post, I looked at the behaviour for \(2 \leq k \leq 5 \). I've looked at the case of \(k=1\) for a wide variety of numbers in several posts back in 2021 so in this post I'm focusing on values of \(k=2\) and looking only at the numbers from 1 to 99. Thus the recursive rule here is:

number --> number + \( \sum d_o^2 - \sum d_e^2 \) 

The trajectory of 1 when \(k=2\) requires 35 steps to reach the loop {327, 381}, acquiring a maximum value of 428 in the process. See Figure 1.

Figure 1

The full details of the trajectory of 1 are as follows:

1, 2, -2, -6, -42, -62, -102, -105, -79, 51, 77, 175, 250, 271, 317, 376, 398, 424, 388, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

The trajectory of 2 is almost identical to that of 1 after only one step (shown in blue):

2, -2, -6, -42, -62, -102, -105, -79, 51, 77, 175, 250, 271, 317, 376, 398, 424, 388, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

The trajectory of 3 eventually overlaps the trajectory of 1 and 2 (shown in blue):

3, 12, 9, 90, 171, 222, 210, 207, 252, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

The trajectory of 4 also overlaps the trajectory of 1 (shown in blue) and is 49 steps in length:

4, -12, -15, 11, 13, 23, 28, -40, -56, -67, -54, -45, -36, -63, -90, -9, 72, 117, 168, 69, 114, 100, 101, 103, 113, 124, 105, 131, 142, 123, 129, 207, 252, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

The trajectory of 5 is quite short, at 22 steps, and it too overlaps the trajectory of 1 (shown in blue):

5, 30, 39, 129, 207, 252, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

The trajectory of 6 is 42 steps long and also overlaps the trajectory of 1 (shown in blue):

6, -30, -21, -24, -44, -76, -63, -90, -9, 72, 117, 168, 69, 114, 100, 101, 103, 113, 124, 105, 131, 142, 123, 129, 207, 252, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

The trajectory of 7 is 29 steps in length and overlaps the trajectory of 1 (shown in blue):

7, 56, 45, 54, 63, 36, 9, 90, 171, 222, 210, 207, 252, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

The trajectory of 8 is 42 steps in length and overlaps the trajectory of 1 (shown in blue):

8, -56, -67, -54, -45, -36, -63, -90, -9, 72, 117, 168, 69, 114, 100, 101, 103, 113, 124, 105, 131, 142, 123, 129, 207, 252, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

The trajectory of 9 is 23 steps in length and overlaps the trajectory of 1 (shown in blue):

9, 90, 171, 222, 210, 207, 252, 269, 310, 320, 325, 355, 414, 383, 337, 404, 372, 426, 370, 428, 344, 321, 327, 381, 327

14 is the next number of interest:

Without listing the trajectories for 10, 11, 12 and 13, it can be noted that all of their trajectories overlap that of 1. However, once we reach 14, there is a new development. The trajectory is 14, -1, 0. What happens of course is that -1 is reached and after that the trajectory is stuck on 0. See Figure 2.

Figure 2

22 and 42  are the next numbers of interest:

After this the trajectories for 15, 16, 17, 18, 19, 20 and 21 all overlap that of 1. Once 22 is reached, the same situation as with 14 prevails. The trajectory of 22 is 22, 14, -1, 0. After 22, all trajectories overlap again with that of 1 until 42 is reached and the trajectory once again plummets to zero: 42, 22, 14, -1, 0, 0.

50 is the next number of interest:

It is only when 50 is reached that we get a new trajectory. See Figure 3.

Figure 3

Once again a loop is reached but this time it is {573, 656, 609, 654, 627, 636}. The full trajectory is:

50, 75, 149, 215, 237, 291, 369, 423, 412, 393, 492, 553, 612, 573, 656, 609, 654, 627, 636, 573

62 and 75 are the next numbers of interest:

From 51 to 61, the trajectories again overlap that of 1 but at 62 it plummets to zero with a trajectory of 62, 22, 14, -1, 0, 0. From 62 to 74, the trajectory overlaps that of 1 until, at 75, the trajectory overlaps that of 50 as can be expected because 50 --> 75:

75, 149, 215, 237, 291, 369, 423, 412, 393, 492, 553, 612, 573, 656, 609, 654, 627, 636, 573

82 and 92 are the next numbers of interest:

From 76 to 81 we're back to overlapping the trajectory of 1 and at 82 we go to zero again with 82, 14, -1, 0, 0. From 83 to 91, we are back to overlapping the trajectory of 1 but at 92 we overlap the trajectory of 50 and 75 (shown in blue):

92, 169, 215, 237, 291, 369, 423, 412, 393, 492, 553, 612, 573, 656, 609, 654, 627, 636, 573

The remaining trajectories for 93 to 99 all overlap the trajectory of 1. These results for the numbers 1 to 99 can be summarised as follows:

• 50, 75 and 92 end in the loop {573, 656, 609, 654, 627, 636}
• 14, 22, 62 and 82 end in 0
• all other numbers end in the loop {327, 381}

The general observation can be made that with \(k=2\) the numbers in the trajectory sequence will eventually rise because any negative odd digits (odd digits always predominate), will become positive when squared. This is not the case of course when \(k=3\) and we will look at this in a subsequent post.

Higher Order Odds and Evens Trajectory

My previous post on higher order Smith numbers gave me the idea to look into what happens with the odd and even trajectory of numbers when the squares of the digits are added or subtracted instead of just the digits themselves. The odd and even rule applied repeatedly to a number\(n\) is simply to add to \(n\) its odd digits and subtract its even ones. I've devoted numerous posts to the analysis of what happens beginning with my post titled Odds and Evens on June 17th 2021.

Numbers whose sum of odd and even digits is equal are not altered when this rule is applied. 112 is an example of such a number and numbers of this type I termed attractors. Other numbers follow a trajectory that either leads them to an attractor or else they enter a loop. Such a loop I termed a vortex and the numbers that comprise a vortex I termed vorticals. 

101 is an example of a number whose trajectory leads to an attractor, in this case 134. Here is its trajectory: 101, 103, 107, 115, 122, 119, 130, 134. 199 is an example of a number that enters a vortex. Its trajectory is 199, 218, 209, 216, 209. Here we see that {209, 216} is the vortex and the vorticals are 209 and 216. Numbers whose trajectories lead to attractors or vortices I've termed captives.

The purpose of this post is to explore what happens when, instead of adding just the odd digit or subtracting the even digit, we add higher powers of those digits. Let's begin by looking at what happens to the number associated with my diurnal age today viz. 26638. Under the odd and even rule, the trajectory is 26638, 26619, 26615, 26607, 26600, 26586, 26569. The trajectory leads to the attractor 26569 that has a total of 92 captives.

What if the squares of the digits are added and subtracted? Well the trajectory then becomes 26638, 26507, 26541, 26511, 26498, 26459, 26509, 26575, 26634, 26551, 26562, 26507 and it can be seen that the trajectory immediately enters a loop or vortex {26507, 26541, 26511, 26498, 26459, 26509, 26575, 26634, 26551, 26562}. 

Let's try with the cubes of the digits. In this case, we end up with an impressively long trajectory:

26638, 25713, 26201, 25970, 27159, 28349, 28521, 28119, 28330, 27864, 27407, 28021, 27494, 28430, 27873, 28066, 27114, 27387, 27580, 27528, 27468, 27011, 27348, 27134, 27433, 27758, 28049, 28194, 28340, 27783, 27976, 29167, 30016, 29828, 29517, 30707, 31420, 31376, 31558, 31324, 31307, 31705, 32201, 32213, 32252, 32380, 31914, 32608, 31899, 32873, 32750, 33237, 33653, 33643, 33444, 33306, 33171, 33570, 34092, 34776, 35209, 36082, 35373, 35922, 36787, 36772, 37261, 37408, 37202, 37556, 37960, 38843, 37809, 38396, 38451, 38028, 37023, 37412, 37711, 38426, 37653, 37959, 39912, 41390, 42083, 41526, 41364, 41048, 40409, 41010, 40948, 41037, 41344, 41180, 40606, 40110, 40048, 39408, 39588, 39445, 40198, 40352, 40432, 40323, 40305, 40393, 41112, 41043, 40943, 41571, 41977, 43329, 44040, 43848, 42723, 43013, 43004, 42903, 43587, 43506, 43378, 43199, 44621, 44270, 44477, 44971, 45916, 46491, 46877, 46771, 47178, 47289, 47777, 49085, 49363, 49866, 49587, 50208, 49813, 49994, 52053, 52322, 52450, 52628, 52009, 52855, 52710, 53171, 53668, 52876, 52608, 51997, 53924, 54733, 55191, 56172, 56417, 56606, 56083, 55507, 56225, 56243, 56107, 56360, 56080, 55477, 56349, 56950, 57713, 58552, 58407, 58299, 59362, 60019, 60533, 60496, 60729, 61577, 62173, 62320, 62115, 62018, 61283, 60575, 60952, 61582, 60972, 61820, 61085, 60483, 59718, 60404, 60060, 59628, 59746, 60663, 60042, 59754, 61012, 60790, 61646, 60935, 61600, 61169, 61468, 60461, 59966, 61117, 61247, 61303, 61142, 60856, 60037, 60191, 60706, 60617, 60529, 61159, 61799, 63385, 62836, 61911, 62427, 62474, 62465, 62086, 61134, 60883, 59670, 60651, 60345, 60217, 60337, 60518, 59916, 61284, 60485, 59818, 59649, 60952

As can be seen, the trajectory of 238 steps finally enters a loop or vortex {60952 ... 59649}. Figure 1 shows a plot of the trajectory.

Figure 1: permalink

When we try with fourth powers we find that the trajectory consists of 599 steps:

26638, 20015, 20625, 19922, 33013, 33257, 36429, 41503, 41954, 48629, 49526, 55144, 55883, 49022, 55295, 63715, 65527, 67866, 62283, 56940, 62574, 64032, 62545, 62227, 63284, 57701, 63129, 68460, 61516, 59551, 67988, 67462, 66999, 84090, 86299, 94013, 100400, 100145, 100516, 99847, 111018, 106926, 110880, 102690, 107940, 116647, 116202, 114876, 111631, 110420, 110150, 110778, 111486, 105841, 102116, 100807, 99113, 112318, 108290, 110740, 112887, 107082, 105372, 108464, 102561, 101876, 98887, 95561, 102077, 106864, 99921, 119589, 129242, 135500, 136832, 131587, 130600, 129386, 130621, 129392, 142564, 141366, 138601, 133292, 139984, 148836, 139174, 147963, 155455, 157700, 163128, 157803, 156815, 152675, 155015, 156892, 158671, 156307, 158119, 161212, 159887, 161283, 155958, 160299, 172110, 174498, 178853, 173769, 183918, 182370, 180741, 178792, 186044, 180141, 175792, 187765, 187801, 182012, 177886, 173201, 175669, 182665, 176587, 176623, 176498, 179813, 184762, 181500, 178031, 176419, 183831, 175803, 174815, 173491, 182280, 174057, 179229, 194721, 203413, 203304, 203194, 209565, 216064, 213201, 213252, 213911, 220540, 220877, 221551, 222771, 227526, 229208, 231625, 231004, 230814, 226528, 221713, 224165, 223207, 225641, 224683, 219084, 221278, 219536, 225492, 232374, 234649, 239467, 246942, 251663, 249762, 257140, 259895, 270155, 273791, 285220, 281701, 279992, 302044, 301597, 311266, 308741, 306872, 303946, 309117, 318162, 312837, 311289, 313821, 309873, 314901, 321289, 323804, 319598, 329331, 336120, 334971, 343840, 339394, 352503, 353899, 363712, 364964, 368502, 363800, 358570, 358206, 353504, 354660, 352518, 349738, 354510, 355586, 352150, 353466, 351405, 352481, 348820, 340437, 342488, 333849, 336301, 335249, 342325, 342824, 338265, 333644, 332079, 341187, 339319, 352685, 348608, 338945, 341941, 348073, 346284, 340445, 340383, 336274, 337269, 345081, 341436, 339791, 355477, 361354, 360590, 366561, 363380, 358231, 354907, 364319, 369491, 381143, 376955, 385952, 389732, 394744, 403019, 409406, 414159, 420835, 417173, 421802, 417419, 425871, 424530, 424708, 422485, 418470, 416264, 413145, 413341, 412993, 425925, 433448, 428746, 425227, 427949, 442944, 448465, 442930, 449044, 454581, 451224, 451306, 450461, 449279, 464274, 464595, 470598, 475833, 474669, 480527, 479185, 484421, 479542, 488601, 478858, 469340, 474174, 478209, 482803, 474420, 476037, 479368, 482763, 479581, 484817, 478515, 477815, 478891, 479406, 486560, 480241, 475618, 472997, 490649, 501963, 507935, 518228, 510630, 510041, 510412, 510767, 514899, 524295, 531818, 524334, 524593, 532213, 532969, 545485, 542752, 546115, 545815, 543339, 550512, 552372, 556072, 558411, 555311, 557269, 566169, 569468, 569710, 578002, 576916, 583912, 587068, 580606, 574543, 577763, 584376, 581835, 574975, 587332, 586408, 577289, 585165, 581649, 583188, 571607, 575739, 588433, 580772, 582087, 576905, 585821, 578864, 572146, 573605, 576041, 577516, 582273, 581252, 578375, 580412, 576670, 579505, 590342, 597337, 609487, 612801, 607395, 615767, 618603, 611997, 626226, 622290, 627507, 631622, 629080, 630233, 629164, 632862, 626223, 623664, 619585, 622005, 621302, 620056, 618073, 615164, 612943, 618018, 608532, 603830, 598600, 600394, 605484, 600205, 599518, 609795, 624647, 623928, 625146, 622908, 624045, 622846, 615870, 613505, 613541, 612697, 619052, 624927, 632305, 631780, 628871, 621769, 628124, 622445, 621230, 619984, 627459, 635478, 632937, 640749, 647903, 655394, 661734, 661369, 664124, 661005, 659039, 671571, 675704, 679579, 696832, 696770, 705541, 708937, 716285, 713904, 722692, 730310, 732874, 733389, 738498, 739093, 754778, 758254, 757537, 766071, 768282, 761163, 761055, 763411, 764343, 765098, 769293, 783585, 779125, 791098, 802526, 797727, 813876, 806871, 799785, 814238, 805856, 797618, 803590, 806761, 802475, 801133, 797201, 808549, 807287, 803881, 791675, 802368, 792945, 808821, 796518, 800714, 798764, 804479, 808833, 796707, 809175, 814667, 810125, 806640, 799696, 819188, 813463, 807978, 811149, 813361, 808133, 800104, 795753, 808447, 802144, 797521, 809494, 818008, 805721, 804636, 797773, 814019, 816230, 810904, 813114, 808846, 795006, 803297, 808228, 795908, 807960, 811530, 808142, 799679, 822868, 809252, 812310, 808281, 795978, 810431, 806162, 799459, 821912, 824347, 822205, 818686, 803807, 798097, 811925, 815001, 811532, 808128, 795825, 801925, 805000, 801529, 804604, 798700, 805967, 810162, 804756, 802134, 797848, 800763, 797853, 805826, 796947, 813319, 815948, 814687, 807345, 806100, 800709, 805575, 805755, 805935, 809731, 814679, 817994, 829166, 829024, 831201, 827172, 827847, 824185, 816347, 813182, 805057, 804612, 798949, 816681, 805899, 811454, 807473, 808004, 799556, 815033, 811725, 810641, 804995, 814390, 816681

Once again, a loop or vortex is entered {816681 ... 814390}. Figure 2 shows a plot of the trajectory.

Figure 2: permalink

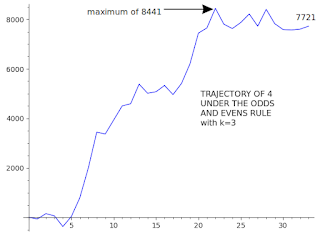
With fifth powers, the trajectory is even longer (971 steps) and, as can be seen, the trajectory initially plunges into negative number territory.

26638, -21471, -37224, -53186, -16011, -8238, 57087, 61058, 23640, 15051, 21303, 21758, 8891, 2405, 4474, 18209, 44459, 103561, 99155, 223504, 225784, 211860, 171286, 147519, 225478, 211554, 216750, 228875, 183207, 167458, 145823, 115368, 78194, 120259, 182370, 166621, 143263, 134918, 160420, 151589, 184122, 150268, 112818, 47253, 66372, 67838, 11576, 23734, 39971, 175120, 195022, 257133, 277520, 314195, 375590, 457939, 595188, 594952, 718244, 700204, 715955, 801187, 752460, 763560, 768183, 711922, 787716, 797594, 951407, 1029365, 1083975, 1130432, 1129864, 1147315, 1166469, 1201168, 1160595, 1218120, 1185291, 1214668, 1165294, 1218638, 1145539, 1210059, 1272203, 1289158, 1285766, 1257347, 1293274, 1368286, 1287410, 1270395, 1349588, 1345446, 1337967, 1423341, 1421749, 1495527, 1576578, 1575899, 1684287, 1626727, 1644726, 1643902, 1694363, 1737323, 1771635, 1800843, 1734527, 1770454, 1805146, 1766705, 1787893, 1815264, 1776791, 1878487, 1812774, 1812566, 1767341, 1792400, 1867201, 1843434, 1808081, 1709779, 1878299, 1947637, 2031744, 2046715, 2057816, 2037173, 2071242, 2086930, 2105646, 2092164, 2142350, 2144631, 2135020, 2138325, 2109105, 2171249, 2246019, 2296205, 2350507, 2373775, 2427775, 2480233, 2446863, 2396706, 2457221, 2476034, 2483228, 2416815, 2378342, 2361779, 2446878, 2388293, 2382228, 2316807, 2293282, 2319678, 2355202, 2361599, 2475258, 2464459, 2515753, 2542147, 2559968, 2643740, 2650934, 2704519, 2782445, 2767497, 2868135, 2798160, 2833441, 2799080, 2901185, 2930561, 2985171, 3031354, 3034185, 3004005, 3006349, 3057084, 3043467, 3050936, 3105820, 3076389, 3112187, 3096440, 3145908, 3174534, 3192905, 3314340, 3313022, 3313688, 3241106, 3232519, 3295116, 3349727, 3441820, 3407216, 3415435, 3420124, 3418256, 3380025, 3350836, 3314146, 3304810, 3271505, 3294774, 3385600, 3348667, 3316616, 3293776, 3379117, 3472268, 3447686, 3414368, 3372263, 3381959, 3470901, 3545977, 3644109, 3693578, 3732501, 3752888, 3674727, 3716559, 3791133, 3867720, 3861001, 3820702, 3804920, 3830388, 3732813, 3717550, 3757658, 3757221, 3794140, 3868192, 3854141, 3822695, 3844504, 3812032, 3779687, 3848856, 3745120, 3764240, 3771434, 3803487, 3754220, 3773307, 3824457, 3809784, 3819323, 3846302, 3805188, 3710253, 3730640, 3739133, 3815962, 3837804, 3788537, 3760226, 3761660, 3755383, 3746401, 3753628, 3733470, 3766789, 3811375, 3799027, 3950950, 4075541, 4096551, 4153051, 4158522, 4130917, 4205994, 4325137, 4344500, 4344796, 4410047, 4423783, 4406228, 4363572, 4375158, 4364667, 4356341, 4350129, 4411491, 4467471, 4490238, 4514682, 4475184, 4459277, 4552985, 4587585, 4547207, 4581866, 4502880, 4439413, 4495877, 4556849, 4579556, 4655987, 4696525, 4745216, 4755293, 4836586, 4757842, 4759733, 4854983, 4849816, 4833506, 4795549, 4934656, 4979473, 5129380, 5158998, 5217811, 5204946, 5257264, 5271457, 5310266, 5298051, 5330551, 5340413, 5341977, 5436985, 5460959, 5576507, 5611720, 5623846, 5577838, 5552409, 5619777, 5724597, 5822454, 5793824, 5839224, 5867785, 5834337, 5821206, 5783724, 5786882, 5700702, 5737409, 5832416, 5794185, 5842500, 5814926, 5835501, 5812352, 5786014, 5764379, 5851610, 5817318, 5771959, 5929922, 6110098, 6128605, 6083379, 6119177, 6204067, 6204266, 6179850, 6218288, 6112145, 6106441, 6088843, 5981982, 6037638, 6006611, 5983285, 5983259, 6075050, 6090331, 6142091, 6192310, 6243796, 6303287, 6280004, 6238404, 6196023, 6239732, 6308234, 6267120, 6268312, 6220172, 6229108, 6247550, 6261775, 6282931, 6301616, 6278533, 6258375, 6241099, 6350366, 6330649, 6373608, 6342581, 6304350, 6299161, 6401677, 6418716, 6386181, 6305338, 6268648, 6178728, 6138999, 6275846, 6246402, 6228738, 6172412, 6180357, 6159989, 6299718, 6394048, 6410748, 6384964, 6393888, 6347343, 6355055, 6360022, 6344649, 6385317, 6365192, 6412026, 6395387, 6434310, 6424973, 6491216, 6533659, 6583892, 6572965, 6639487, 6666242, 6634050, 6620842, 6571434, 6581786, 6520631, 6508416, 6462198, 6471872, 6463887, 6398825, 6387898, 6357917, 6446173, 6445624, 6430093, 6480828, 6373692, 6434450, 6426970, 6486218, 6404075, 6414183, 6371836, 6340810, 6299486, 6368208, 6287331, 6264049, 6305466, 6284482, 6209058, 6230656, 6210664, 6186281, 6105163, 6092981, 6170504, 6181637, 6150369, 6197235, 6268652, 6215617, 6219967, 6339289, 6417297, 6501129, 6555497, 6631928, 6642869, 6644766, 6628421, 6579014, 6649196, 6742943, 6809186, 6787148, 6746427, 6762409, 6821657, 6793238, 6829004, 6846453, 6799453, 6928926, 6998640, 7067394, 7151500, 7174559, 7272449, 7363000, 7372517, 7426275, 7454150, 7475160, 7503100, 7523276, 7552418, 7541652, 7555878, 7533331, 7554236, 7568704, 7563875, 7563438, 7542288, 7495596, 7627951, 7715932, 7811932, 7855233, 7845976, 7900196, 8027326, 8003768, 7947506, 8034494, 8057946, 8095359, 8187182, 8105655, 8074487, 8040517, 8026658, 7948663, 7975418, 8037415, 8023799, 8126147, 8101356, 8064182, 7989815, 8062310, 8021978, 8032267, 8008709, 8019029, 8104328, 8037980, 8048543, 7984327, 8043409, 8067885, 7981737, 8058683, 7955971, 8113934, 8139679, 8234284, 8166879, 8161648, 8079538, 8093226, 8111910, 8138195, 8135078, 8089718, 8067271, 8060310, 8020010, 7987211, 8047076, 8039122, 8065583, 7998764, 8108908, 8069654, 8082484, 7982100, 8025157, 8015415, 7987875, 8034934, 8059653, 8084651, 8013441, 7978870, 8022804, 7956180, 7994618, 8087956, 8093625, 8115466, 8069249, 8145747, 8147671, 8139719, 8242101, 8208247, 8158430, 8095239, 8183905, 8180787, 8116098, 8101837, 8053353, 8027564, 8005896, 7994758, 8115803, 8053637, 8033511, 8004356, 7966156, 8021810, 7956244, 8025369, 8047210, 8030194, 8055695, 8083575, 8041339, 8067083, 8010821, 7945255, 8029430, 8054898, 8017744, 8016543, 7978344, 8036434, 7994328, 8095652, 8120375, 8107751, 8111724, 8094710, 8136775, 8133214, 8099878, 8136479, 8171011, 8155054, 8130638, 8057813, 8012453, 7981998, 8110417, 8093435, 8122303, 8089958, 8112877, 8080925, 8077531, 8081746, 8024218, 7957595, 8118682, 8012572, 7999673, 8202901, 8229119, 8314387, 8265121, 8227640, 8202815, 8140341, 8105770, 8109742, 8151775, 8158873, 8080745, 8034117, 8017377, 8035274, 8021625, 7984143, 8025427, 8011503, 7982105, 8028287, 7946726, 8022781, 7973989, 8152225, 8125612, 8088131, 7990072, 8141752, 8127862, 8071294, 8113327, 8097822, 8108078, 8026582, 7956331, 8028023, 7962666, 8007386, 7951124, 8029051, 8058426, 7987183, 8014554, 7985989, 8117532, 8104909, 8189216, 8174923, 8217199, 8319306, 8338298, 8299497, 8459627, 8497008, 8506304, 8468104, 8392745, 8438145, 8373930, 8417747, 8433353, 8403658, 8332690, 8351649, 8372499, 8473823, 8424524, 8391745, 8437178, 8404476, 8377667, 8380011, 8314720, 8297947, 8415835, 8355769, 8397574, 8459813, 8455671, 8437161, 8412645, 8373147, 8373456, 8352306, 8315341, 8285162, 8214912, 8240107, 8223091, 8249552, 8280995, 8336650, 8291941, 8376217, 8369499, 8505321, 8479015, 8524205, 8496599, 8635303, 8598613, 8587719, 8617972, 8670060, 8638547, 8584386, 8480650, 8409439, 8492964, 8568438, 8464702, 8438885, 8310157, 8297566, 8328195, 8325045, 8297714, 8356554, 8324604, 8282223, 8216802, 8143427, 8125630, 8088423, 7989306, 8083910, 8077667, 8079768, 8099119, 8243500, 8213044, 8178440, 8127664, 8095096, 8175775, 8199679, 8353090, 8382982, 8343906, 8361873, 8305855, 8249937, 8351261, 8314055, 8286757, 8250152, 8223571, 8210915, 8240291, 8265485, 8197367, 8249730, 8292005, 8321347, 8304817, 8255308, 8196233, 8215193, 8244812, 8177165, 8173362, 8150080, 8087670, 8047972, 8106811, 8033502, 8004313, 7971008, 8030904, 8056404, 8016937, 8052493, 8081086, 7975007, 8087602, 8031065, 7993890, 8155319, 8188095, 8151966, 8165822, 8095572, 8144878, 8061334, 8020253, 7990789, 8168782, 8079478, 8105581, 8046297, 8080553, 8021510, 7991837, 8111025, 8081353, 8019429, 8103704, 8086963, 8065167, 8036780, 7980518, 7993964, 8179361, 8214918, 8207377, 8225241, 8194479, 8294569, 8374192, 8416468, 8333333, 8302023, 8269677, 8313988, 8275220, 8262288, 8156112, 8118664, 8036554, 8001479, 8043544, 8011072, 7995081, 8100344, 8065772, 8061935, 8083809, 8044797, 8102644, 8060021, 8019446, 8035904, 8064529, 8085103, 8022936, 8041620, 8000021, 7967222, 8052013, 8022582, 7960075, 8048087, 7965566, 8024344, 7988715, 8018968, 7971938, 8091126, 8109601, 8128108, 8029774, 8088613, 7982777, 8076254, 8054586, 7986500, 8024937, 8067212, 8043412, 8008808, 7877736, 7904663, 7964186, 7990699, 8235926, 8257735, 8265042, 8226535, 8192420, 8217614, 8192823, 8186516, 8108555, 8052395, 8085137, 8039777, 8116722, 8092923, 8178432, 8128891, 8089606, 8067567, 8055986, 8047973, 8107087, 8075166, 8046779, 8097874, 8123977, 8184084, 8083733, 8035733, 8023626, 7975485, 8040606, 7991262, 8118328, 8020237, 8004455, 7975889, 8065190, 8086821, 7980710, 8040606

The trajectory once again enters a loop {8040606 ... 7980710}. Figure 3 shows the trajectory.

Figure 3: permalink

I'll leave off there and powers higher than 5 may prove rather unwieldy. It's not possible to make generalisations at this early stage but it would seem that the trajectories are far more volatile and lengthy once we start dealing with powers of digits. The trajectories may end up favouring vortices instead of attractors. 

One general observation is that the trajectories will always tend to rise rather than fall because there are the odd digits (1, 3, 5, 7 and 9) with an average value of 5 outweighing the even digits (0, 2, 4, 6, 8) with an average value of 4.