Third Order Odds and Evens Trajectory for Numbers 1 to 10.

My previous post was titled Second Order Odds and Evens Trajectory for Numbers 1 to 99 and in this post I will be looking at the behaviour of the numbers from 1 to 10 under the recursive rule:

number --> number + \( \sum d_o^3 - \sum d_e^3 \) 

where \( d_o^3 \) are the number's odd digits raised to the power \( 3\) and \( d_e^3 \) are the number's even digits raised to the power \( 3\).  There is more variability with the numbers when \(k=3\) so I'm restricting my analysis to just the numbers from 1 to 10. A full analysis from 1 to 99 would be too lengthy but this is the beginning of the third order analysis and I'll follow up with more numbers in a future post.

Figure 1 shows the trajectory for the number 1. The entire trajectory consists of 161 steps and begins with 1, 2, -6, 210, 203, 222, 198, ... . The numbers that are in the final loop are {-7721, -8400, -7824, -7583, -7566, -7602}. The minimum value reached is -8441.

Figure 1

Here we see how the power of 3 drives the trajectory into increasingly negative territory until there is a brief rally after which the loop is reached.

 

2 is on exactly the same trajectory as 1 since 1 --> 2 under the odds and evens rule.

3 has a brief trajectory of only 14 steps: 3, 30, 57, 525, 767, 1237, 1600, 1385, 1026, 803, 318, -166, 265, 166, -265, -166 and ends in the loop {-166, 265, 166, -265}. See Figure 2.

Figure 2

30 and 57 also lie on the path of 3 and thus end in the same {-166, 265, 166, -265} loop.

4 follows a similar pattern to 1 and 2 except that the maximum value is +8441 and the loop is the same except that the members are positive {7721, 8400, 7824, 7583, 7566, 7602}. See Figure 3.

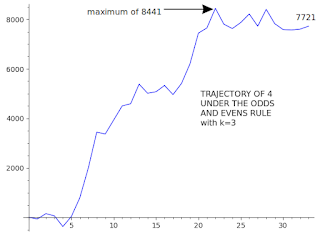Figure 3

5 and 6 and 7 have lengthy trajectories but eventually end up in the same positive loop as 4.

8 produces a new trajectory that plummets to a record low of -34870 and ends in the loop {-34203, -34185, -33762, -33935, -34870, -34664, -34131, -34123, -34106, -33854, -33457, -33915, -34824} after 169 steps. See Figure 4.

Figure 4

9 follows a similar trajectory to 1 and 2 ending in the negative loop {-7721, -8400, -7824, -7583, -7566, -7602}.

10 follows a similar trajectory to 4, 5, 6 and 7 ending in the positive loop {7721, 8400, 7824, 7583, 7566, 7602}. 

So in summary:

• 1, 2 and 9 end in the loop {-7721, -8400, -7824, -7583, -7566, -7602}.
• 3 ends in the loop {-166, 265, 166, -265}.
• 4, 5, 6, 7 and 10 end in the loop {7721, 8400, 7824, 7583, 7566, 7602}. 
• 8 ends in the loop {-34203, -34185, -33762, -33935, -34870, -34664, -34131, -34123, -34106, -33854, -33457, -33915, -34824}.