Zeroes of the Mertens Function

I examined the Möbius and Mertens functions in a post titled The Möbius Function and Mertens Function on January 25th 2020. In number theory, we define the Mertens function as:$$M(n) = \sum_{1\le k \le n} \mu(k)$$where \( \mu (k)\) is the Möbius function. For any positive integer n, \(μ(n)\) has values in {−1, 0, 1} depending on the factorisation of \(n\) into prime factors:$$\mu(n) = \begin{cases} 1 & \quad \text{if } n \text{ is square-free + integer with even number of prime factors}\\ -1 & \quad \text{if } n \text{ is square-free + integer with odd number of prime factors}\\ 0 & \quad \text{if } n \text{ has a squared prime factor} \end{cases}$$

In that earlier post, I plotted the Mertens function for values up to one million but in this post I want to look at a smaller range and focus on the zeroes of the function in that range. Figure 1 shows a plot of the  Mertens function for values between 25500 and 26080.

Figure 1

We see that in this range, the zeroes occur at in a run of three (25514, 25515, 25516) and later singly (26077).  I'm focusing on this range because these numbers are in the vicinity of my current diurnal age which is 26634 as of March 5th 2022. I'm afraid I've missed these previous zeroes in my daily number analysis because they don't register in a search of the OEIS unless you're looking at b-files.

The zeroes of the Mertens function comprise OEIS A028442:

A028442

Numbers \(k\) such that Mertens's function M(\(k\)) (A002321) is zero.

The initial values are:

2, 39, 40, 58, 65, 93, 101, 145, 149, 150, 159, 160, 163, 164, 166, 214, 231, 232, 235, 236, 238, 254, 329, 331, 332, 333, 353, 355, 356, 358, 362, 363, 364, 366, 393, 401, 403, 404, 405, 407, 408, 413, 414, 419, 420, 422, 423, 424, 425, 427

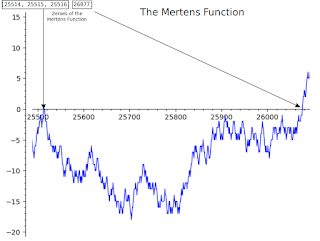
Figure 2 shows a further range from 26000 to 26750 where there a lot more zeroes:

Figure 2

Here the zeroes are:

26077, 26134, 26142, 26146, 26153, 26154, 26162, 26163, 26164, 26177, 26179, 26180, 26181, 26183, 26184, 26263, 26264, 26266, 26269, 26273, 26277, 26279, 26280, 26282, 26285, 26321, 26346, 26349, 26350, 26427, 26428, 26430, 26434, 26443, 26444, 26446, 26449, 26450, 26451, 26452, 26454, 26710

The zero upcoming for me is 26710 which is not that far off (Friday, May 20th 2022). After that there is not another zero until Tuesday, April 30th 2024 which is more than two years away. This distant zero will occur as the first in a closely spaced series: 27421, 27429, 27431 and 27432. After that, there is a large gap. See Figure 3.

Figure 3

The full list of zeroes is as follows:

27421, 27429, 27431, 27432, 27922, 27939, 27940, 27973, 27977, 28009, 28011, 28012, 28014, 28018, 28021, 28031, 28032, 28033, 28122, 28127, 28128, 28155, 28156, 28183, 28184, 28189, 28191, 28192, 28193, 28202, 28221, 28254, 28259, 28260, 28262, 28283, 28284, 28290, 28551, 28552, 28554, 28558, 28562, 28565, 28566, 28567, 28568

I find the Mertens function oddly fascinating and its graph certainly resembles the graph of cumulative random coin tosses where a tail counts as -1 and a head as +1. In the graph of the Mertens function however, the graph can run along the \(x\) axis for a bit because any number with repeated prime factors counts as 0.

For example, consider the run of zeroes 26449, 26450, 26451, 26452 where we have:

• 26449 = 26449 which has \( \mu \) = -1 which brings the graph to the \(x\) axis
• 26450 = 2 * 5^2 * 23^2 which has \( \mu \) = 0 so graph stays on \(x\) axis
• 26451 3^2 * 2939 which has \( \mu \) = 0 so graph stays on \(x\) axis
• 26452 2^2 * 17 * 389 which has \( \mu \) = 0 so graph stays on \(x\) axis

Once we reach 26453 = 7 * 3779 we have \( \mu \) = 1 and we leave the \(x\) axis.

OEIS A319520 records increasing runs of zero in the Mertens function:

A319520

Starts of strictly increasing runs of 0's in Mertens's function A002321.

The initial members of the sequence are 2, 39, 331, 422, 45371, 22898822, 871469945 ... where we have:

• 2 is a term because M(2) = 0 for a run of one zero
• 39 is a term because M(39) = M(40) = 0 for a run of two zeroes
• 331 is a term because M(331) = M(332) = M(333) = 0 for a run of three zeroes
• 422 is a term because M(422) = ... = M(425) = 0 for a run of four of four zeroes
• 45371 is a term because M(45371) = ... = M(45376) = 0 for a run of six zeroes

Figure 4 shows the graph of the Mertens function in the vicinity of 45371 to 45376:

Figure 4: permalink