Ultramagic Squares

Here is a definition of an ultramagic square:

A magic square is associative if the sum of any two elements symmetric about its center is the same. A magic square is pandiagonal if the sum of the numbers in any broken diagonal equals the magic constant. A magic square is ultramagic if it is associative and pandiagonal. Ultramagic squares exist for orders n>=5. Source.

Using this as a starting point, let's understand what is meant by a pandiagonal magic square. Here is a definition taken from a most useful website:

Pandiagonal magic squares are magic squares, where also the broken diagonals sum to the magic constant. This means when you go off of one edge on a diagonal, continue (wrap-around) to the corresponding cell on the opposite edge. These squares are considered as one of the top classes of magic squares.

Figures 1 and 2 show clearly what is meant by a "broken diagonal" and show a 5 x 5 magic square that is pandiagonal. 

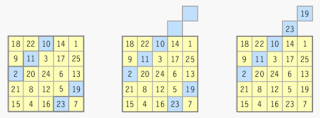Figure 1

Figure 2

The magic square in Figures 1 and 2 however, is not associative. Using the central square (24) as a reference point, we note that, up-down 3 + 12 = 15 but left-right 20 + 6 = 26. These must be equal for a magic square to be associative. Figure 3 shows a 5 x 5 magic square that is both pandiagonal and associative, and thus ultramagic.

Figure 3

The magic constant for this square is 65 and it can be seen that all rows, columns, main diagonals and broken diagonals all add to this number. Furthermore, the up-down 6 + 20 = 26 and the left-right 2 + 24 = 26 are this time equal as are all the other symmetric pairs of elements.

Figure 3 shows a 7 x 7 ultramagic square:

Figure 4: source

Figures 5, 6 and 7 show 6 x 6, 7 x 7 and 8 x 8 prime ultramagic squares with magic constants of 990, 4613 and 2040 respectively:

Figure 5: source

Figure 6: source

Figure 8: source

These magic constants (990, 4613 and 2040) are the lowest possible and form part of OEIS A257316:

A257316

Smallest magic constant of ultramagic squares of order \(n\) composed of distinct prime numbers.

The sequence runs 3505, 990, 4613, 2040 with 3505 being the magic constant (not shown) for the 5 x 5 ultramagic square with minimal magic constant. The following bounds for the next terms are known:

• 12249 <=a(9) <=13059
• 4200 <=a(10) <=46150
• a(11) >= 26521
• a(12) >= 8820
• a(13) >= 49439
• a(14) >= 16170
• a(15) >= 74595
• a(16) >= 21840

My attention was attracted to the topic because today I turned 26521 days old and this number happens to be the lower bound for the 11 x 11 prime ultramagic square with minimal magic constant. The exact composition of such a square is presumably still not known.

My earlier posts on Magic Squares are:

• Magic Squares on 21st September 2020
• Prime Semi-Magic Squares on 7th May 2021
• Anti-Magic Squares on 17th July 2018