Apocalyptic Numbers

X-Men: Apocalypse (2016)

Numbers Aplenty has to say about apocalyptic numbers:

A number of the form $2^n$ is called apocalyptic if its digits contain "666" as a substring. The smallest apocalyptic number is $2^{157}$, which is equal to:

$$182687704\underline{666}362864775460604089535377456991567872$$ while $2^{220}$ is the smallest apocalyptic number which contains two 666 groups, being equal to: $${\tiny 168499\underline{66666}969149871\underline{666}88442938726917102321526408785780068975640576}$$ The smallest power of 2 with 3 groups is $2^{931}$.

A number $n$ such that $2^n$ is apocalyptic is called an apocalyptic power or apocalyptic exponent.

Between $1$ and $3 \times 10^6$ there are 3715 numbers which are non-apocalyptic exponents, the largest being 29784. In other words, it is highly probable that $2^n$ for $n \ge 29785$ is an apocalyptic number.

Probably there are only 8 numbers, namely 2666, 3666, 5666, 6660, 6665, 6669, 11666, 26667 which contains 666 among their digits but are not apocalyptic exponents.

The first apocalyptic exponents are 157, 192, 218, 220, 222, 224, 226, 243, 245, 247, 251, 278, 285, 286, 287, 312, 355, 361, 366, 382, 384, 390, 394, 411, 434, 443, 478, 497, 499, 506, ...

Here is a link to the first 1000 apocalyptic exponents. As the numbers get larger, the frequency of numbers being non-apocalyptic exponents decreases so that, after 29874, the frequency is (probably) zero. For example, in the range from 20000 to 30000, there are only the following non-apocalyptic exponents:

20271, 20300, 20509, 20644, 20710, 21077, 21600, 21602, 22447, 22734, 23097, 23253, 24422, 24441, 25026, 25357, 25896, 26051, 26667, 29784

Why this interest in apocalyptic numbers? Well, in my diurnal age count, I've entered what might be termed an "apocalyptic phase". I'm currently 26606 days old and heading toward 26666 (the latter occurs a day before my 73rd birthday). Interestingly, as can be seen in the range of numbers above, 26667 is the second last non-apocalyptic exponent.

Numbers Aplenty also shows the smallest 3 × 3 magic square made of consecutive apocalyptic numbers. See Figure 1.

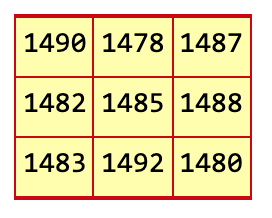Figure 1

The apocalyptic powers comprise OEIS A007356:

A007356

Apocalyptic powers: $2^n$ contains $666$.

Finally, let's not forget that:

Georg Cantor was born on the 3rd March 1845 in St Petersburg, Russia, and died on the 6th January 1918 in Halle, Germany. At the time of this death, he was 72 years 10 months and 3 days old or 72.85 years of age which is equivalent to 26606 days.

Georg Cantor

This is the exact age that I am today.