Necklaces and Bracelets

At my recent diurnal age of 25136 (I'm 25138 days old as I write this), I noted that:

25236 is also a member of OEIS A141783: number of bracelets (turn over necklaces) with n beads: 1 blue, 12 green, and r = n-13 red (here n=20 and so r=7). This can be restated as "the number of bracelets with 1 blue, 12 green and 7 red beads is 25236". 

I had trouble understanding why the number of bracelets was 25236 and not 25194. According to my initial calculations, the number of necklaces (arrangements of beads that can't be lifted out of the plane and reversed) should be 19!/(12!*7!) = 50388. Here the numerator is 19! because 20!/20 adjusts for the rotational symmetry of the twenty beads and the denominator takes into account the fact that the beads in each of the groups, 12 green and 7 red, are indistinguishable from one another. Because bracelets can be lifted out of the plane and turned over, the number of bracelets should be 50338/2 = 25194.

As with most things, it's better to start at the beginning. The sequence runs: 1, 7, 49, 231, 924, 3108, 9324, 25236, ... and begins with n=13 at which point there is only one possible configuration as there are no red beads. When n=14, there is one red bead, one blue bead and twelve green beads. I would reckon the number of possible necklace configurations to be: 13!/12!=13 but in fact there is one more as can be seen in Diagram 1 and 2:

Diagram 1: blue bead on left, red bead on right

Diagram 2: red bead on left, blue bead on right.

As the two diagrams show, the first configuration with a blue bead on the left and a red bead on the right can be rotated to produce a new configuration where the red bead is on the left and the blue bed is on the right. This means that there are 13+1=14 possible necklaces and thus 14/2=7 possible bracelets.

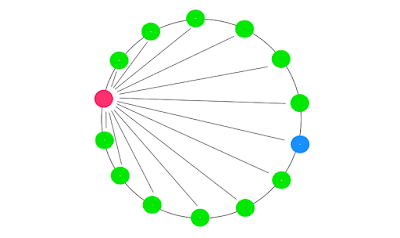
When there are 20 beads, the situation is of course more complicated but the principle is the same. There will be the 50388 necklaces as calculated above but there are also the extra necklaces created by rotating the blue and red beads by 180° for the symmetric configurations like the one shown in Diagram 3. In every symmetric configuration, there will be nine beads (six green and three red) on either side of the red-blue bead axis. There are \( \binom{9}{3} = 84 \) ways this can be done and so the total number of necklaces is 50388+84=50472, corresponding to 50472/2=25236 bracelets.

Diagram 3: a symmetrical position with green and red

identically placed on either side of the red-blue axis