Constants Associated with Centered Hexagonal and Other Figurate Numbers

Today I turned 25669 days old and this number happens to be the 93rd centered hexagonal number. These are figurate numbers because they can be represented as hexagonal rings surrounding a central dot. See Figure 1.

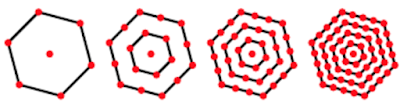Figure 1

Centered hexagonal numbers can be written in the form \(3 \,n \, (n-1)+1\) where \(n=0,1,2,3, ... \). What struck me as interesting were some of the properties of this series which begins: 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919, 1027, 1141, 1261, ... I'm thankful to NumbersAplenty for alerting me to these properties. See Figure 2.

Figure 2: http://www.numbersaplenty.com/set/hex_number/

These results are quite amazing. The property on the left in Figure 2, I'll designate as property 1, the one in the middle as property 2 and the one on the right as property 3.

Property 1

Let's consider the sequence up to the 93rd hexagonal number and see how the results compare:$$ \sum_1^{93}{\frac{1}{H_n}} \approx 1.30169996966629 \text{ and } \frac{\pi \,\tanh{\frac{\pi}{2\sqrt{3}}}}{\sqrt{3}} \approx 1.50944975010619$$Given that the last term in the sequence on the left is 1/25669 \( \approx \) 0.0000389574973703689, there are clearly a great many more terms to add before the figure on the right is approached.

Property 2

By contrast, this sequence approaches 13 fairly rapidly:$$ \sum_1^{93} \frac{H_n}{2^n} \approx 12.9999999999999999999999972942$$Property 3

Notice that the summation begins at \(n=0\) and this is confusing because \(H_0\) is not really defined. It might be better to begin the summation at \(n=1\) and make the right side equal to \(4e-1\). In this case, the summation on the left again rapidly approaches the value on the right (not surprising in view of the factorial in the denominator):$$ \sum_1^{93} \frac{H_n}{n!} = 4e -1\text{ to at least 100 decimal places}$$There are interesting results for the sums of the reciprocals of other figurate numbers. Some of these are shown in Figure 3 (heptagonal), Figure 4 (octagonal) and Figure 5 (decagonal).

Figure 3: http://www.numbersaplenty.com/set/heptagonal_number/

Figure 4: http://www.numbersaplenty.com/set/octagonal_number/

Figure 5: http://www.numbersaplenty.com/set/decagonal_number/

There are plenty more but that's enough for the moment. In the meantime, the centered hexagonal and other figurate numbers have been shown to be linked to the mathematical constants \(\pi \) and \(e\), yet another example of the connectivity of numbers that I discussed in my previous post.