A Special Complete Bipartite Graph

In December of 2024, I made a post titled Welcoming In 2025 in which I looked at some of the more interesting properties of the number 2025. Recently, in this YouTube video, I came across another interesting property of the number in connection to complete bipartite graphs and spanning trees.

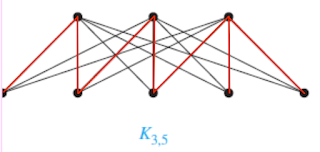
The definition of a complete bipartite graph is a graph where all possible edges connect vertices in two disjoint sets, but no edge connects vertices in the same set. An example is $K_{3,5}$ shown in Figure 1. The two disjoint sets have 3 and 5 vertices, hence the nomenclature.

A spanning tree is defined as a graph that connects all of a graph's vertices without creating any loops or cycles. It's a subgraph of the original graph, meaning it uses all of the vertices but only some of the edges.

An example of a spanning tree for $K_{3,5}$ is shown in Figure 2 where the red edges represent the spanning tree.

There is a general formula for calculating the number of spanning trees for a $K_{m.n}$ bipartite graph and it is:$$s(K_{3,5})=m^{n-1}{n}^{m-1}$$So in the case of $K_{3,5}$ we have:$$s(K_{3,5})=3^4{5}^2=2025$$Thus there are 2025 spanning trees for a complete $K_{3,5}$ bipartite graph and thus we have another interesting property of this year's number.