Up and Down the Mountain

The number (27532) associated with my diurnal age today has an interesting aliquot sequence consisting of 210 steps that reaches a maximum value of 210998991785527991104 before beginning its descent to 1 and then 0. Here is the sequence:

27532, 20656, 19396, 17256, 25944, 43176, 80664, 121056, 224688, 378448, 494512, 495504, 1012336, 1181968, 1182960, 2995344, 6599280, 14542224, 25693296, 43014360, 90683160, 185451240, 425275800, 940708200, 1975489080, 4299600360, 9787608600, 30598377960, 62464790040, 124929580440, 322138579560, 782543654040, 1590997194600, 3789466067640, 8612422885320, 17245450814520, 34491361043400, 72967727801400, 156608347258440, 511373352229560, 1193233352540040, 3238776242618040, 7557144566112360, 17008403414134680, 43343078672652120, 98245289952891720, 225485753448117420, 499595022460258740, 1016220356878620060, 2146302511659329220, 4365805465306640340, 8912079582213674700, 19057572060429045492, 30451944343316954508, 46523803857845347256, 43522269061507054024, 41538397982866392056, 39514226617193027944, 34588280875055182556, 26164545907884419524, 19879736397904788476, 15278939116317231844, 13034324430483320084, 9787165489989868000, 14259900118915247504, 13373492843095311856, 12537649540401854896, 11754756084394941888, 20702681104040261952, 35918311240577926848, 63312611494171175232, 104258325352849123008, 210998991785527991104, 207702132538879116370, 169624609562080576430, 135726953604303765970, 148468761008721086318, 131290689970046993554, 93931702661206931822, 67094073456072645490, 63039859860977978510, 66642137567319577426, 33622680034706422574, 20453938384323035986, 10514105806833405614, 5257053195212561074, 2628558999616292174, 1319289459782004154, 678859735840149446, 432198199089642970, 372584654387623790, 423185411483397010, 447367434996734126, 335199506688516274, 241133173013919566, 129392986488928594, 69210234498425006, 49442455265686354, 31628275705499822, 17569420012749490, 15482802556130510, 12912073075113586, 8615431262813582, 4307715631406794, 2182074293639066, 1091037352376614, 545519846484554, 272807528144026, 136403764072016, 172028060840272, 246230032928432, 322698987259984, 302536923800196, 440536222376284, 330402166782220, 469768933828340, 521929534249180, 574124185108340, 632252256474700, 811995150775220, 893194665852784, 856062512768896, 913869490270304, 885311068699420, 1142969402332388, 857227051749298, 428613525874652, 321536752958884, 279499971575516, 235369388238244, 208212125817436, 207269989503284, 155452492127470, 125699432957330, 100559546365882, 50279927860454, 25488855451066, 20776630073990, 21985463380090, 25902201396614, 14856456204922, 7434249373850, 7457427003070, 7186247839538, 4160459275582, 2399770256450, 2707938109054, 1364410976426, 711333048214, 360723394754, 183945042814, 115353159818, 74577627382, 39307973018, 20226433030, 16181146442, 8167141114, 5307725702, 2873228938, 1532896886, 800767234, 435474206, 217915858, 109021742, 58683250, 51172262, 26101738, 16062650, 15625798, 8569082, 5026822, 2524250, 2417830, 1934282, 1381654, 746954, 459706, 282938, 144250, 126254, 63130, 53510, 42826, 39254, 22786, 11396, 14140, 20132, 20188, 21308, 21364, 22526, 16114, 11534, 6226, 3998, 2002, 2030, 2290, 1850, 1684, 1270, 1034, 694, 350, 394, 200, 265, 59, 1, 0

Figure 1 shows these values plotted on a logarithmic vertical scale that necessarily ends in 1 not 0 because we are working with logarithms. The sequence is embedded in the graph.

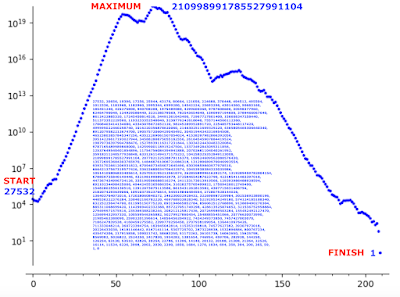Figure 1: permalink (not annotated)

The logarithmic graph is preferable to the non-logarithmic because of the massive spike that makes the smaller values invisible. See Figure 2.

Figure 2: permalink

In an earlier post the 15th August 2024, I posted about Infinite, Aperiodic Aliquot Series but this series is finite as shown but takes a while to terminate. I'll continue to monitor the aliquot sequences generated by the numbers associated with my diurnal age and report on any that involve a large number of steps to terminate or for which no termination can be demonstrated.

In earlier posts, I've mentioned aliquot sequences of various types. These posts include:

• Aliquot Sequences on 20th December 2017
• Aliquot Sequences Revisited on 21st June 2021
• Periodic Unitary Aliquot Sequences on 30th September 2023
• The Lehmer Five on 17th May 2024
• Infinite, Aperiodic Aiquot Sequences on 15th August 2023