If we envisage a semiprime that is not a square number as a rectangle then a number like 15 that is equal to 3 x 5 could be represented as shown in Figure 1:
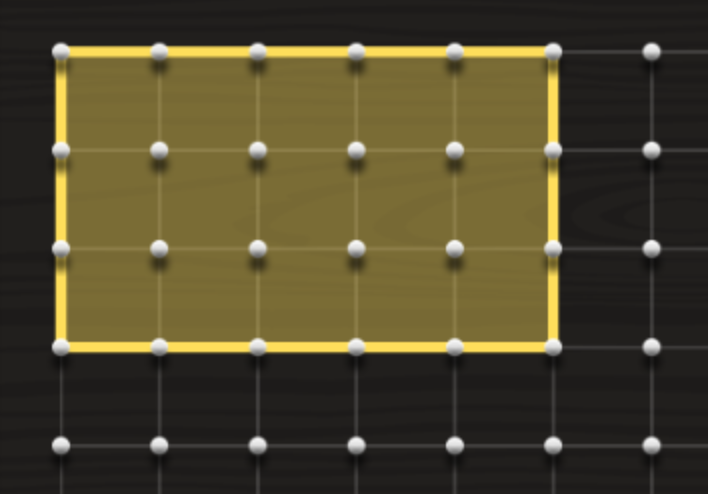 |
Figure 1: created using Geoboard |
The average of 3 and 5 is 4 and a 4 x 4 square has the same perimeter as the 3 x 5 rectangle. Both are 16 units in perimeter. See Figure 2.
Though the rectangle and the square have the same perimeter, they have different areas. The rectangle has an area of 15 square units and the square has an area of 16 square units. 16 is a square number and the semiprime 15 is linked to it via its two prime factors:$$\frac{3 +5}{2} \times 4 = 16$$The square number divided by 4 gives the side of the associated square. Not every semiprime can be linked to square number in this way. Take 33 with prime factors of 3 and 11 as an example:$$\frac{3 +11}{2} \times 4 = 28$$In general, if a semiprime has two distinct prime factors \(a\) and \(b\), then the condition is that \(2 \times (a+b) \) needs to be a square number.
In the range up to 40,000, only 172 of the 9790 semiprimes qualify (permalink). Here is the list:
15, 65, 77, 87, 141, 247, 301, 335, 481, 589, 591, 671, 717, 767, 785, 1007, 1167, 1247, 1271, 1351, 1415, 1501, 1527, 1661, 1937, 1967, 2071, 2077, 2157, 2257, 2317, 2391, 2977, 3007, 3047, 3101, 3197, 3215, 3439, 3997, 4061, 4087, 4237, 4385, 4487, 4607, 4829, 4927, 5111, 5777, 6031, 6077, 6161, 6487, 6497, 6541, 6557, 6751, 6927, 7087, 7265, 7341, 7357, 7361, 7967, 8189, 8479, 8557, 9217, 9271, 9287, 9517, 9991, 10077, 10157, 10231, 10727, 11041, 11327, 12209, 12687, 12877, 12989, 13511, 13847, 14317, 14397, 15007, 15185, 15917, 16081, 16397, 16769, 16897, 16957, 17711, 17951, 18141, 18157, 18527, 18807, 19117, 19127, 19367, 19511, 19679, 19741, 19757, 20017, 20191, 20567, 20687, 20711, 20877, 21041, 21421, 21697, 23015, 23231, 23377, 23389, 23729, 23839, 24727, 24737, 24887, 24961, 25341, 25661, 25837, 25967, 25985, 26797, 26909, 27341, 27661, 28247, 28417, 29047, 29135, 29431, 30237, 30311, 30461, 30847, 31597, 31681, 32047, 32551, 32567, 32847, 33527, 34207, 34241, 34647, 34951, 35249, 35741, 35807, 36077, 36391, 36737, 37327, 37437, 37777, 38081, 38191, 38407, 38551, 38687, 39421, 39665
Let's test the second member of the sequence, 65, with factors of 5 and 13. We see that:$$2 \times (5+13)=36$$The associated square has a side of 9 units. However, different semiprimes can produce the same square number. Take the semiprime 77 with prime factors of 7 and 11 as an example: $$2 \times (7+11)=36$$See Figure 3 where the two rectangles associated with the two different semiprimes are shown together with the associated square.
 |
Figure 3: created using Geoboard |
If we want to work backwards from the square numbers to the semiprimes, then it's a question of dividing the square number by 2 and partitioning the resultant number into two parts such that each is prime. The results (permalink) are shown in the table below with only those semiprimes up to 40,000 displayed. The algorithm is easily modified so as to remove this filter and show all semiprimes associated with square numbers up and including 40,000.
square half-square rectangle semiprime 16 8 [5, 3] 15 36 18 [13, 5] 65 36 18 [11, 7] 77 64 32 [29, 3] 87 64 32 [19, 13] 247 100 50 [47, 3] 141 100 50 [43, 7] 301 100 50 [37, 13] 481 100 50 [31, 19] 589 144 72 [67, 5] 335 144 72 [61, 11] 671 144 72 [59, 13] 767 144 72 [53, 19] 1007 144 72 [43, 29] 1247 144 72 [41, 31] 1271 196 98 [79, 19] 1501 196 98 [67, 31] 2077 196 98 [61, 37] 2257 256 128 [109, 19] 2071 256 128 [97, 31] 3007 256 128 [67, 61] 4087 324 162 [157, 5] 785 324 162 [151, 11] 1661 324 162 [149, 13] 1937 324 162 [139, 23] 3197 324 162 [131, 31] 4061 324 162 [109, 53] 5777 324 162 [103, 59] 6077 324 162 [101, 61] 6161 324 162 [89, 73] 6497 324 162 [83, 79] 6557 400 200 [197, 3] 591 400 200 [193, 7] 1351 400 200 [181, 19] 3439 400 200 [163, 37] 6031 400 200 [157, 43] 6751 400 200 [139, 61] 8479 400 200 [127, 73] 9271 400 200 [103, 97] 9991 484 242 [239, 3] 717 484 242 [229, 13] 2977 484 242 [223, 19] 4237 484 242 [211, 31] 6541 484 242 [199, 43] 8557 484 242 [181, 61] 11041 484 242 [163, 79] 12877 484 242 [139, 103] 14317 576 288 [283, 5] 1415 576 288 [281, 7] 1967 576 288 [277, 11] 3047 576 288 [271, 17] 4607 576 288 [269, 19] 5111 576 288 [257, 31] 7967 576 288 [251, 37] 9287 576 288 [241, 47] 11327 576 288 [229, 59] 13511 576 288 [227, 61] 13847 576 288 [199, 89] 17711 576 288 [191, 97] 18527 576 288 [181, 107] 19367 576 288 [179, 109] 19511 576 288 [157, 131] 20567 576 288 [151, 137] 20687 576 288 [149, 139] 20711 676 338 [331, 7] 2317 676 338 [307, 31] 9517 676 338 [277, 61] 16897 676 338 [271, 67] 18157 676 338 [241, 97] 23377 676 338 [229, 109] 24961 676 338 [211, 127] 26797 676 338 [199, 139] 27661 676 338 [181, 157] 28417 784 392 [389, 3] 1167 784 392 [379, 13] 4927 784 392 [373, 19] 7087 784 392 [349, 43] 15007 784 392 [331, 61] 20191 784 392 [313, 79] 24727 784 392 [283, 109] 30847 784 392 [241, 151] 36391 784 392 [229, 163] 37327 784 392 [211, 181] 38191 784 392 [199, 193] 38407 900 450 [443, 7] 3101 900 450 [439, 11] 4829 900 450 [433, 17] 7361 900 450 [431, 19] 8189 900 450 [421, 29] 12209 900 450 [419, 31] 12989 900 450 [409, 41] 16769 900 450 [397, 53] 21041 900 450 [389, 61] 23729 900 450 [383, 67] 25661 900 450 [379, 71] 26909 900 450 [367, 83] 30461 900 450 [353, 97] 34241 900 450 [349, 101] 35249 900 450 [347, 103] 35741 900 450 [337, 113] 38081 1024 512 [509, 3] 1527 1024 512 [499, 13] 6487 1024 512 [439, 73] 32047 1024 512 [433, 79] 34207 1156 578 [571, 7] 3997 1156 578 [547, 31] 16957 1156 578 [541, 37] 20017 1156 578 [499, 79] 39421 1296 648 [643, 5] 3215 1296 648 [641, 7] 4487 1296 648 [631, 17] 10727 1296 648 [619, 29] 17951 1296 648 [617, 31] 19127 1296 648 [607, 41] 24887 1296 648 [601, 47] 28247 1296 648 [587, 61] 35807 1444 722 [719, 3] 2157 1444 722 [709, 13] 9217 1444 722 [691, 31] 21421 1600 800 [797, 3] 2391 1600 800 [787, 13] 10231 1600 800 [769, 31] 23839 1600 800 [757, 43] 32551 1764 882 [877, 5] 4385 1764 882 [863, 19] 16397 1764 882 [859, 23] 19757 1764 882 [853, 29] 24737 1764 882 [839, 43] 36077 1936 968 [937, 31] 29047 2116 1058 [1051, 7] 7357 2116 1058 [1039, 19] 19741 2116 1058 [1021, 37] 37777 2304 1152 [1129, 23] 25967 2304 1152 [1123, 29] 32567 2500 1250 [1237, 13] 16081 2500 1250 [1231, 19] 23389 2916 1458 [1453, 5] 7265 2916 1458 [1451, 7] 10157 2916 1458 [1447, 11] 15917 2916 1458 [1439, 19] 27341 3136 1568 [1549, 19] 29431 3364 1682 [1669, 13] 21697 3364 1682 [1663, 19] 31597 3600 1800 [1789, 11] 19679 3600 1800 [1787, 13] 23231 3600 1800 [1783, 17] 30311 4096 2048 [2029, 19] 38551 4356 2178 [2161, 17] 36737 4624 2312 [2309, 3] 6927 4900 2450 [2447, 3] 7341 4900 2450 [2437, 13] 31681 5184 2592 [2579, 13] 33527 5476 2738 [2731, 7] 19117 6084 3042 [3037, 5] 15185 6724 3362 [3359, 3] 10077 7056 3528 [3517, 11] 38687 7396 3698 [3691, 7] 25837 8464 4232 [4229, 3] 12687 9216 4608 [4603, 5] 23015 9604 4802 [4799, 3] 14397 10000 5000 [4993, 7] 34951 10404 5202 [5197, 5] 25985 11664 5832 [5827, 5] 29135 12100 6050 [6047, 3] 18141 12544 6272 [6269, 3] 18807 13924 6962 [6959, 3] 20877 15876 7938 [7933, 5] 39665 16900 8450 [8447, 3] 25341 20164 10082 [10079, 3] 30237 21904 10952 [10949, 3] 32847 23104 11552 [11549, 3] 34647 24964 12482 [12479, 3] 37437
One could extend this idea to sphenic numbers and three dimensions. Each sphenic number can be interpreted as a brick or rectangular prism. What sphenic numbers have surface areas that are the same as that of cubes with integer sides? The list of such sphenic numbers is shown in the table below (permalink):
sphenic factors SA cube side SA 374 2 * 11 * 17 486 9 486 710 2 * 5 * 71 1014 13 1014 3110 2 * 5 * 311 4374 27 4374 3590 2 * 5 * 359 5046 29 5046 4454 2 * 17 * 131 5046 29 5046 6182 2 * 11 * 281 7350 35 7350 7190 2 * 5 * 719 10086 41 10086 8911 7 * 19 * 67 3750 25 3750 9494 2 * 47 * 101 10086 41 10086 10502 2 * 59 * 89 11094 43 11094 10507 7 * 19 * 79 4374 27 4374 11798 2 * 17 * 347 13254 47 13254 18518 2 * 47 * 197 19494 57 19494 18854 2 * 11 * 857 22326 61 22326 20390 2 * 5 * 2039 28566 69 28566 24134 2 * 11 * 1097 28566 69 28566 27559 7 * 31 * 127 10086 41 10086

No comments:
Post a Comment