Unremarkable Numbers

Every now and again, as I track my diurnal age, I come across a number that is, for want of a better word, unremarkable. 26534 appears to be such a number. It has two entries in the OEIS and both of them are of the inscrutable variety. Searches elsewhere reveal nothing meaningful either. 

Such apparent "duds" can serve as a stimulus to really look at the number more closely in an effort to extract some properties of interest. In the case of 26534, two properties came to light when I did this. These are:

• each of its five digits is unique (2, 6, 5, 3, 4)
• the digits when ordered are sequential (2, 3, 4, 5, 6)

This becomes important when tracking my diurnal age because, in the span of 10000 numbers from 20000 to 29999, there are very few numbers with this property. There are 120 permutations of the five digits (2, 3, 4, 5, 6) but if we fix the 2 in place then there are only 24 numbers that lie in this range from 20000 to 29999. These are:

23456, 23465, 23546, 23564, 23645, 23654, 24356, 24365, 24536, 24563, 24635, 24653, 25346, 25364, 25436, 25463, 25634, 25643, 26345, 26354, 26435, 26453, 26534, 26543

As can be seen, 26534 is the penultimate number when such numbers are ordered and the final number, 26543, is only nine days away. Another group of 24 numbers can be found for the range from 20000 to 29999 using the digits 1, 2, 3, 4, 5 by fixing the 2 in first place. The numbers in this group are:

21345, 21354, 21435, 21453, 21534, 21543, 23145, 23154, 23415, 23451, 23514, 23541, 24135, 24153, 24315, 24351, 24513, 24531, 25134, 25143, 25314, 25341, 25413, 25431

Using the digits from 0 to 4 and again fixing the 2 in first place, we get another 24 digits in the range from 20000 to 29999. These are:

20134, 20143, 20314, 20341, 20413, 20431, 21034, 21043, 21304, 21340, 21403, 21430, 23014, 23041, 23104, 23140, 23401, 23410, 24013, 24031, 24103, 24130, 24301, 24310

Altogether then there are 72 numbers in the range from 20000 to 29999 that meet the criteria:

• each digit in unique
• the digits when ordered are sequential

Thus, out of 10000 numbers, only 0.72% satisfy the criteria. It turns out that 26534 is rather special after all. Here is a permalink that can be used to generate these numbers.

Star Numbers Revisited

 So called Star Numbers are few and far between. Up to 40,000, they are:

1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, 937, 1093, 1261, 1441, 1633, 1837, 2053, 2281, 2521, 2773, 3037, 3313, 3601, 3901, 4213, 4537, 4873, 5221, 5581, 5953, 6337, 6733, 7141, 7561, 7993, 8437, 8893, 9361, 9841, 10333, 10837, 11353, 11881, 12421, 12973, 13537, 14113, 14701, 15301, 15913, 16537, 17173, 17821, 18481, 19153, 19837, 20533, 21241, 21961, 22693, 23437, 24193, 24961, 25741, 26533, 27337, 28153, 28981, 29821, 30673, 31537, 32413, 33301, 34201, 35113, 36037, 36973, 37921, 38881, 39853

Today I happened to turn 26533 days old which is why my attention was drawn to them again. I had posted about these numbers in an eponymous blog post on 7th June 2019. On that occasion I was writing about the star number 25741 that was 109 days away at that point. I was surprised to see that this post came up in fourth position when the phrase "star numbers" was entered into the Google search bar (see Figure 1):

Figure 1

It also attracted two comments that I only just noticed (see Figure 2). I'm reminded that I should check my various blogs for comments on a regular basis, something that I've quite neglected.

Figure 2

In this post I want to look at some interesting properties of this sequence that I didn't cover in that earlier post. The first involves a result for the sum to infinity of the reciprocals of the star numbers:$$ \sum_{n=1}^{\infty} \frac{1}{S_n}=\frac{\pi \tan{\dfrac{\pi}{2 \sqrt{3}}}}{2 \sqrt{3}} \approx 1.15917331963217$$The second infinite sum involves the factorial function:$$ \sum_{n=0}^{\infty} \frac{S_n}{n!}=7 e$$The third infinite sum involves powers of 2:$$ \sum_{n=1}^{\infty} \frac{S_n}{2^n}=25$$These results are listed in Numbers Aplenty but no proofs are supplied, so I'm just listing them here. Wolfram MathWorld supplies a generating function for the star numbers:

It also provides a linear recurrence relation:  

The star numbers form OEIS :

A003154

Centered 12-gonal (dodecagonal) numbers. Also star numbers: 6*n*(n-1) + 1.

In the comments to this sequence in the OEIS, the diagram shown in Figure 3 appears:

Figure 3

So that's about it. In summary, this post is simply meant to supplement my earlier post and I would encourage anyone reading this post to read that as well, because it contains many other interesting facts about star numbers.

Numbers As Sums Of Palindromes

I've written about palindromes before in a variety of posts (just type palindromes into the search box for this site) but thus far I've not mentioned the representation of numbers as a sum of palindromes. Figure 1 shows a screenshot of a tweet from Cliff Pickover's Twitter feed:

Figure 1

I came across this tweet not long ago and immediately wrote a program (permalink) in SageMathCell to determine what these palindromic sums were for any given number. Below is the calculation box.

It turns out that for 26532, my diurnal age today, there are 193 different way to represent it as a sum of three palindromes. Here are examples of just a few of them:

• 11 + 969 +25552
• 414 + 7337 + 18781
• 979 + 1111 + 24442
• 5885 + 6006 + 14641

Most numbers, about 92%, can in fact be represented as a sum of two palindromes in one or more ways. However, 26532 is amongst the 8% minority that cannot. The numbers on either side of it however, can be represented as a sum of two palindromes. The program above can be easily modified to find these palindromes, just replace C = Combinations(P, 3) with C = Combinations(P, 2). Here are the results:

• 26531 = 979 + 25552
• 26533 = 171 + 26362 = 1991 + 24542

Between 26500 and 27000, the numbers that cannot be represented as a sum of two palindromes are:

26502, 26512, 26522, 26532, 26542, 26572, 26582, 26592, 26602, 26612, 26622, 26632, 26642, 26672, 26682, 26692, 26702, 26712, 26722, 26732, 26742, 26772, 26782, 26792, 26802, 26812, 26822, 26832, 26842, 26872, 26882, 26892, 26902, 26912, 26922, 26932, 26942, 26952, 26972, 26982, 26992

There are 41 such numbers representing 8.20% of the total of 500 numbers. It can be noted that all the numbers in this range are even and all end in 2. This pattern seems to repeat for other ranges. 

That's about it, a simple yet interesting property that divides numbers into two categories: those that can be represented as a sum of two palindromes and those that cannot. 

888

PHYSICS

Figure 1: neutron decays into proton, electron and neutrino

Triple 8 is a most interesting number for a variety of reasons. However, today I stumbled upon the number is an unexpected context. In an article in UNIVERSE TODAY dated 11th November 2021, it's stated that:

Together with protons, neutrons make up the nuclei of the atoms we see around us. Within an atomic nucleus, neutrons can be extremely stable. But when a neutron is on its own, it typically decays in a matter of minutes. 

There are a couple of ways we can measure neutron half-life, such as measuring a beam of neutrons or cooling them down and trapping them in a magnetic bottle, but these different methods give different results for the half-life. The methods should give the same result, but they don’t. The beam method gives a lifetime of 888 seconds, while the bottle method gives 879 seconds.

Perhaps there is some systematic error in the methods, but this discrepancy is a problem for fundamental physics. But a new study has measured neutron decay in a third way, by using a spacecraft orbiting the Moon.

The airless surface of the moon is constantly bombarded by cosmic rays. Sometimes a cosmic ray will kick a neutron off the lunar surface. As the neutron speeds away from the Moon, it has a chance of decaying. So the team used NASA’s Lunar Prospector satellite to count the number of neutrons at various orbital heights. From this, they calculated the neutron lifetime to be 887 seconds.

So the decay time may not be exactly 888 seconds but the beam method returns this result. 

LUCK

What are some other contexts in which these triple digits occur? The Wikipedia article on the topic says that:

In Chinese numerology, 888 usually means triple fortune, as s form a strengthening of the digit 8. On its own, the number 8 is often associated with great fortune, wealth and spiritual enlightenment. Hence, 888 is considered triple. For this reason, addresses and phone numbers containing the digit sequence 888 are considered particularly lucky, and may command a premium because of it.

Several online gambling sites incorporate the number:

• 888casino: formerly Casino-on-Net, is an online casino founded in 1997 and based in Gibraltar. It is one of the Internet's oldest casinos, and in 2013 it became the first exclusively online casino to be licensed in the United States.
  
  
• 888 Holdings PLC, (LSE: 888) known commonly as 888.com, is a public company which owns several popular gambling brands and websites. 888 is based in Gibraltar. It is listed on the London Stock Exchange and is a constituent of the FTSE 250 Index. The business was founded in May 1997 by Israeli entrepreneurs Avi and Aaron Shaked and Shay and Ron Ben-Yitzhak, two sets of brothers, as Virtual Holdings Limited. 
  
  
• 888poker, formerly Pacific Poker, is an international online poker card room and network owned by 888 Holdings. 888poker was established in 2002, and is based in Gibraltar.
  
  
• 888sport (pronounced as "Triple Eight Sport") is a multinational online sports gambling company headquartered in Gibraltar. It was founded in 2008 and is a subsidiary of 888 Holdings plc. The company provides online sports betting, predominantly in European markets.

MATHEMATICS

• There is an 888math.com website that offers tutoring at $8.88 per hour.
  
  
  
  
  
• Mathematically, \(888^3 = 700227072\) is the smallest cube in which each digit occurs exactly three times. The list up to one million of such numbers is (permalink):

888, 56592, 58524, 65577, 70869, 78183, 496941, 512427, 516267, 517461, 557949, 565920, 581421, 585558, 661959, 711828, 713772, 723627, 724983, 733053, 739563, 764472, 781830, 877242, 988458

• It is the only cube in which three digits occur three times. For example, the next number in the previous sequence (56592) has a cube of 181244621426688 but there are four digits that occur three times.
  
  
• 888 the smallest multiple of 24 whose digit sum is 24 and, as well as being divisible by its digit sum, it is divisible by all of its digits.
  
  
• 888 and 24 show up again in the former's membership of OEIS 236661 where 888 counts the number of partitions of 24 that have a standard deviation greater than 2. Permalink.
  
  
• 888 can be written using four 4's:    \(4!+\dfrac{4! \times 4!}{\sqrt{.4}}\)
  
• Other properties of the number include its being a happy, Harshad, Moran, nude, strobogrammatic, modest, congruent, amenable, practical, abundant, pseudoperfect and Zumkeller number (see Numbers Aplenty).
  
  
• The 8's are involved in 888 again thanks to its membership of OEIS A127335.
  
  

A127335

Numbers that are the sum of 8 successive primes.

 The sequence runs:

77, 98, 124, 150, 180, 210, 240, 270, 304, 340, 372, 408, 442, 474, 510, 546, 582, 620, 660, 696, 732, 768, 802, 846, 888

The eight successive primes in the case of 888 are 97, 101, 103, 107, 109, 113, 127 and 131 with an average of 111. Both 111 and 888 are of course repdigits along with the infamous 666 or number of the beast.

• 888 arises in the context of aliquot sequences via OEIS A014360:
  
  

A014360

Aliquot sequence starting at 552.

The sequence begins:

552, 888, 1392, 2328, 3552, 6024, 9096, 13704, 20616, 30984, ...

To quote from Wolfram Alpha:

It has not been proven that all aliquot sequences eventually terminate and become periodic. The smallest number whose fate is not known is 276. There are five such sequences less than 1000, namely 276, 552, 564, 660, and 966, sometimes called the "Lehmer five". 

LABOUR

The three 8's are associated with the labour movement as shown in Figure 2:

Figure 2

CHRISTIANITY

The number is strongly associated with Jesus as well via Greek language Gematria:

Figure 3

The close connection between 666 and 888 can be seen in Figure 4 that features the solar magic square. I've written about the magic squares of the Sun, Moon and planets in a previous blog most titled Magic Squares.

Figure 4: source

Figure 5 shows how the two numbers, 666 and 888, are closely linked. In the diagram, the circled numbers on the magic square form the Greek letter “X” which is the “sign” of Christ. The sum of all the numbers in the field of the magic square of the sun (666) added to the sum of the numbers in the twelve Christ circles (222) is equal to the number of Jesus (888).

Figure 5: source

Figure 6 explores the 888 connection with Jesus even further. It should be remembered that the New Testament was written originally in Greek. To quote:

The 24 letters of the Greek alphabet has an 8-8-8 structure. The first row of eight letters represent units, the second row of eight letters represent tens, the third row of eight letters represent hundreds. If you look inside any Greek dictionary you will see this 8-8-8 letter-number table. Every literate Greek person alive during the time of Christ knew it.

The Greek alphabet was invented almost one thousand years before the birth of Jesus. At the time it was invented, every one of the 24 letters in the Greek alphabet represented a number as well as a sound. Since every name and word in the Greek language had a corresponding numerical value, words could be expressed as numbers and numbers could be expressed as words.  This made the Greek alphabet a public cipher and immediately encouraged two numerical practices called Isopsephia and gematria. 

Isopsephia is the practice of converting words and names into numbers. Gematria is the practice of converting numbers into geometry. The number value of "Jesus" is "888." The above circle has a circumference of 888 units, the same value as the 8-8-8 table structure inscribed inside it. Can anyone honestly believe the authors of the gospels did not use this alphabetic cipher tool when they sat down to write? Source.

Figure 6: source

SYNCHRONICITY

Synchronicity struck this morning on my morning walk when I came across the car number plate B 888 AVJ. This is the morning immediately following my post of the previous day. I'd never seen this number plate before, as far as I remember, and I often note car number plates during my walks.

Ultramagic Squares

Here is a definition of an ultramagic square:

A magic square is associative if the sum of any two elements symmetric about its center is the same. A magic square is pandiagonal if the sum of the numbers in any broken diagonal equals the magic constant. A magic square is ultramagic if it is associative and pandiagonal. Ultramagic squares exist for orders n>=5. Source.

Using this as a starting point, let's understand what is meant by a pandiagonal magic square. Here is a definition taken from a most useful website:

Pandiagonal magic squares are magic squares, where also the broken diagonals sum to the magic constant. This means when you go off of one edge on a diagonal, continue (wrap-around) to the corresponding cell on the opposite edge. These squares are considered as one of the top classes of magic squares.

Figures 1 and 2 show clearly what is meant by a "broken diagonal" and show a 5 x 5 magic square that is pandiagonal. 

Figure 1

Figure 2

The magic square in Figures 1 and 2 however, is not associative. Using the central square (24) as a reference point, we note that, up-down 3 + 12 = 15 but left-right 20 + 6 = 26. These must be equal for a magic square to be associative. Figure 3 shows a 5 x 5 magic square that is both pandiagonal and associative, and thus ultramagic.

Figure 3

The magic constant for this square is 65 and it can be seen that all rows, columns, main diagonals and broken diagonals all add to this number. Furthermore, the up-down 6 + 20 = 26 and the left-right 2 + 24 = 26 are this time equal as are all the other symmetric pairs of elements.

Figure 3 shows a 7 x 7 ultramagic square:

Figure 4: source

Figures 5, 6 and 7 show 6 x 6, 7 x 7 and 8 x 8 prime ultramagic squares with magic constants of 990, 4613 and 2040 respectively:

Figure 5: source

Figure 6: source

Figure 8: source

These magic constants (990, 4613 and 2040) are the lowest possible and form part of OEIS A257316:

A257316

Smallest magic constant of ultramagic squares of order \(n\) composed of distinct prime numbers.

The sequence runs 3505, 990, 4613, 2040 with 3505 being the magic constant (not shown) for the 5 x 5 ultramagic square with minimal magic constant. The following bounds for the next terms are known:

• 12249 <=a(9) <=13059
• 4200 <=a(10) <=46150
• a(11) >= 26521
• a(12) >= 8820
• a(13) >= 49439
• a(14) >= 16170
• a(15) >= 74595
• a(16) >= 21840

My attention was attracted to the topic because today I turned 26521 days old and this number happens to be the lower bound for the 11 x 11 prime ultramagic square with minimal magic constant. The exact composition of such a square is presumably still not known.

My earlier posts on Magic Squares are:

• Magic Squares on 21st September 2020
• Prime Semi-Magic Squares on 7th May 2021
• Anti-Magic Squares on 17th July 2018 

Semiprime Triples

I track the properties of the number associated with my diurnal age using Airtable and today I noticed an interesting pattern. See Figure 1.

Figure 1

Referring to Figure 1, it can be seen that I'm experiencing a run of three consecutive semi-primes. I thought I'd investigate how frequent such runs were. I'm regarding a semi-prime as a number that is the product of two distinct prime numbers and thus excluding square numbers like 121. It should also be pointed at that a run of four consecutive semi-primes is not possible. OEIS A039833 uses the smallest of the semi-primes to mark such patterns:

A039833

Smallest of three consecutive square-free numbers \(k, k+1, k+2\) of the form \(p \times q\) where \(p\) and \(q\) are primes.

Up to 1000, there are 13 such triplets with the first being (33, 34, 35):

• (33, 34, 35)
• (85, 86, 87)
• (93, 94, 95)
• (141, 142, 143)
• (201, 202, 203)
• (213, 214, 215)
• (217, 218, 219)
• (301, 302, 303)
• (393, 394, 395)
• (445, 446, 447)
• (633, 634, 635)
• (697, 698, 699)
• (921, 922, 923)

This gives a frequency of 1.3%. Tracking the frequency in powers of 10 (starting with 100) produces the following results: 

• 2 in the first 100, a percentage of 2%
• 13 in the first 1,000, a percentage of 1.3%
• 71 in the first 10,000, a percentage of 0.71%
• 379 in the first 100,000, a percentage of 0.379%
• 2377 in the first 1,000,000, a percentage of 0.2377%

This is shown in Figure 2 using a log scale for the horizontal axis.

Figure 2: permalink

These results are not surprising because as the numbers get larger, it is less likely that they'll have only two distinct prime factors. It would seem that, asymptotically, the frequency approaches zero.

The next such triple is not far off, being (26581, 26582, 26583). It should be pointed out that all semi-prime triples must have one number with 2 as a factor and another number with 3 as a factor. These two numbers must be consecutive in either order. The third number, either the smallest or largest of the triple, will be a semi-prime that does not have 2 or 3 as a factor. Let's use this triple as an example:

• 26581 = 19 x 1399
• 26582 = 2 x 13291
• 26583 = 3 x 8861

Mention should be made of the situation where two semi-prime triples are separated by a single number (which must always be divisible by 36). The first such pair of triples is (213, 214, 215) and (217, 218, 219) where the dividing number 216 = 6 x 36. OEIS A202319 uses the middle semi-prime in the first member of the pair to mark such patterns (thus 214 is the first member):

A202319

Lesser of two semi-primes sandwiched each between semi-primes thus forming a twin semi-prime triple.

The initial members of the sequence are:

214, 143098, 194758, 206134, 273418, 684898, 807658, 1373938, 1391758, 1516534, 1591594, 1610998, 1774798, 1882978, 1891762, 2046454, 2051494, 2163418, 2163958, 2338054, 2359978, 2522518, 2913838, 3108202, 4221754, 4297318, 4334938, 4866118, 4988878, 5108794

Reuleaux Triangle

Today, having turned 26518 days old, I found an interesting property of this number that qualifies it for membership in OEIS A340644:

A340644

The number of vertices on a Reuleaux triangle formed by the straight line segments mutually connecting all vertices and all points that divide the sides into \(n\) equal parts.

 The initial members of the sequence are:

3, 19, 120, 442, 1332, 2863, 5871, 10171, 17358, 26518, 40590, 57757, 81735, 110209, 148158, 192184, 248772, 313105, 393429, 483283, 593490, 715528, 861660, 1022281, 1211811, 1418515, 1659108, 1919842, 2220204, 2543527, 2912751, 3308305, 3755922, 4233730, 4770150, 5340529, 5977071

26518 corresponds to the case where \(n=10\) and Figure 1 illustrates the situation:

Figure 1: source

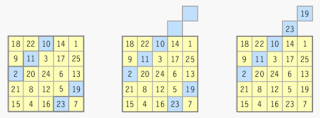
The vertices referred to are best illustrated in the simplest non-trivial case of \(n=2\) where 19 vertices can be counted. See Figure 2.

Figure 2: source

The Reuleaux triangle has some very interesting properties but first a definition from Wikipedia:

A Reuleaux triangle is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its centre on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because all its diameters are the same, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

Figures 3 and 4 illustrate what is mentioned in the definition:

Figure 3: Wikipedia

Figure 4: Wikipedia

The Reuleaux triangle has the smallest possible area of any curve of given constant width. This area is:$$ \frac{1}{2}(\pi - \sqrt{3}) \, s^2 \approx 0.77477 \, s^2 \text{ where } s \text{ is the constant width}$$At the other extreme, the curve of constant width that has the maximum possible area is a circular disk, which has area given by:$$ \frac{\pi \, s^2}{4} \approx 0.78540 \, s^2$$Wikipedia goes on to say that:

Any curve of constant width can form a rotor within a square, a shape that can perform a complete rotation while staying within the square and at all times touching all four sides of the square. However, the Reuleaux triangle is the rotor with the minimum possible area. As it rotates, its axis does not stay fixed at a single point, but instead follows a curve formed by the pieces of four ellipses. Because of its 120° angles, the rotating Reuleaux triangle cannot reach some points near the sharper angles at the square's vertices, but rather covers a shape with slightly rounded corners, also formed by elliptical arcs. Figure 5 illustrates this.

Figure 5

Interestingly, we also learn from the same source that:

Many guitar picks employ the Reuleaux triangle, as its shape combines a sharp point to provide strong articulation, with a wide tip to produce a warm timbre. Because all three points of the shape are usable, it is easier to orient and wears less quickly compared to a pick with a single tip.

Figure 6: source

To quote from the site:

APC™ Trident Pick

$35.00

The APC™ Trident is our take on an historic shape used by acoustic guitar players, electric players as well as mandolin players. This shape also has an interesting property, it is a curve with a consistent width also known as a Reuleaux triangle. The world’s first guitar pick that is true Reuleaux triangle. It can roll smoothly.

Another application of the shape, to quote again from Wikipedia, is:

The Reuleaux triangle has been used as the shape for the cross section of a fire hydrant valve nut. The constant width of this shape makes it difficult to open the fire hydrant using standard parallel-jawed wrenches; instead, a wrench with a special shape is needed. This property allows the fire hydrants to be opened by firefighters (who have the special wrench) but not by other people trying to use the hydrant as a source of water for other activities. Figure 7 illustrates this.

Figure 7

Clifford Pickover in his famous "The Math Book" has a section on the Reuleaux Triangle in which he writes:

Reuleaux Triangle 

Franz ReuIeaux (1829-1905)

The Reuleaux triangle (RT) is one example of a wide class of geometrical discoveries like the Mobius Strip that did not find many practical applications until relatively late in humankind's intellectual development. Not until around 1875, when the distinguished German mechanical engineer Franz Reuleaux discussed the famous curvy triangle, did the RT begin to find numerous uses. Although Reuleaux wasn't the first to draw and consider the shape formed from the intersection of three circles at the comers of an equilateral triangle, he was the first to demonstrate its constant-width properties and the first to use the triangle in numerous real-world mechanisms. The construction of the triangle is so simple that modem researchers have wondered why no one before Reuleaux had exploited its use. The shape is a close relative of a circle because of its constant width, meaning that the distance between two opposite points is always the same.

Various technology patents have focused on drill bits that cut square holes using the RT. At first, the notion of a drill that creates nearly square holes defies common sense. How can a revolving drill bit cut anything but a circular hole? But such drill bits exist For example, the illustration shown here is from the 1978 patent U.S. 4,074,778 for a "Square Hole Drill" and is based on the RT. The RT also appears in patents for other drill bits as well as for novel bottles, rollers, beverage cans, candles, rotatable shelves, gearboxes, rotary engines, and cabinets.

Many mathematicians have studied the Reuleaux triangle, so we know a lot about its properties. For example, its area is \( A = \frac{1}{2}(\pi - \sqrt{3}) \, r^2 \) and the area drilled by a RT drill bit covers 0.9877003907... of the area of an actual square. The small difference occurs because the Reuleaux drill bit produces a square with very slightly rounded corners. Figure 8 illustrates the patent design.

Figure 8

The Reuleaux Triangle also appears is architecture, especially Church architecture where it represents the Trinity. Figure 9 depicts a Reuleaux triangle shaped window of Sint-Salvatorskathedraal, Bruges.

Figure 9: source

Figure 10 shows the Trefoil knot, associated with the Borromean Rings. The Reuleaux Triangle is in the centre together with the three overlapping each being a vesica pisces.

Figure 10

This is just a small sampling of the properties and applications relating to the Reuleaux Triangle and much more could be written but I'll have to stop somewhere. 

Trilinear Coordinates

I'm familiar with Cartesian coordinates and polar coordinates but only recently encountered trilinear coordinates in the context of triangles. See Figure 1.

Figure 1

In Figure 1, it can be seen that the point P is a perpendicular distance a', b' and c' from the sides a, b and c respectively. Working with Cartesian coordinates would require that the triangle be placed and oriented on the Cartesian plane. However, our interest is really on the distances a', b' and c' and even here it's not that actual distances but ratio of the distances. This is where trilinear coordinates come to our assistance.

The trilinear coordinates are written as ka' : kb' : kc' where k is any positive constant, chosen so that the ratio is in its simplest form. Point P in any triangle that is similar to that shown in Figure 1 can be associated with these trilinear coordinates. Figure 2 shows a different triangle in which the point P is external to the triangle.

Figure 2

Here the line AC or b lies between P and the vertex B. However, the lines AB or c and BC or a do not lie between the respective vertices C and A. In such a situation, kb' is given a negative sign whereas ka' and kc' are positive. Here are the trilinear coordinates for some common points:

• A = 1 : 0 : 0
  
  
• B = 0 : 1 : 1
  
  
• C = 0 : 0 : 1
  
  
• incentre = 1 : 1 : 1
  (the centre of the circle that has the triangle sides as tangents)
  
  
• centroid = bc : ca : ab = 1/a : 1/b : 1/c = cosecA : cosecB : cosecC
  (the point where the medians meet)
  
  
• circumcentre = cosA : cosB : cosC
  (the centre of the circle that passes through the three vertices)
  
  
• orthocentre = secA : secB : secC
  (the point where the altitudes meet)

There are many more points associated with triangles but this is a start. Note how the trilinear coordinates or trilinears as they are sometimes called can be expressed in terms of the sides of the triangle or the angles opposite these sides. Figure 3 shows the situation for the centroid (marked G) where AX, BY and CZ are medians.

Figure 3

Remember that the medians of a triangle, divide it into six smaller triangles of equal area. Looking at Figure 3, it can be seen that:

• Area of ∆AGC = Area of ∆AGB = Area of ∆BGC
• 1/2 x b x b' = 1/2 x c x c' = 1/2 x a x a'
• bb'=cc' and so b'/c'=c/b or b':c'=c:b or b':c'=ac:bc
• cc'=aa' and so c'/a'=a/c or c':a'=a:c or c':a'=ab:bc
• a':b':c'=bc:ac:ab=1/a:1/b:1/c
• a/sinA=b/sinB=c/sinC and so a:sinA=b:sinB=c:sinC
• a':b':c'=1/a:1/b:1/c=1/sinA:1/sinB:1/sinC=cosecA:cosecB:cosecC

Figure 4 shows a specific example of the trilinear coordinates for a right-angled triangle with angles of 30° and 60°.

Figure 4

References: 

• Triangle Convertor for Cartesian, Trilinear and Barycentric Coordinates
• Trilinear coordinates (Wikipedia)
• Trilinear Coordinates (MathWorld)