Palindromic Cyclops Numbers

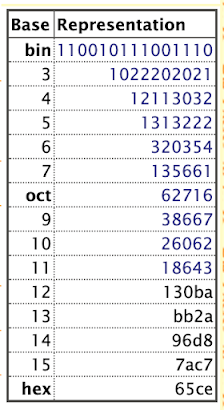
The photo pretty well sums up how I'm feeling today and today is a palindromic cyclops number day. I'm currently 26062 days old. My last such day was obviously 25052 and my next will be 27072. Mathematically, there is nothing deeply significant about such numbers. They are a peculiarity of the base ten number system. In other number bases, the number is not palindromic, as can be seen in Figure 1:

Figure 1: source

By contrast, primeness is intrinsic to the number itself and is independent of the base being used to express the number. The base-dependent peculiarities however, still exert a powerful fascination over numberphiles. Figure 2 shows a fancy font representation of 26062. Sometimes it's nice to just enjoy the symmetry of a number and to admire its representation in an artistic font.

Figure 2: created from https://www.fontspace.com/kingthings-willow-font-f6912

In a more mathematically appreciative world, people might celebrate their palindromic cyclic days in the same way that they celebrate their birthdays. They only occur about every three years, so they are rather special. Instead, these days pass by unnoticed for most of humanity. In 600 days time, I'll turn 26662 days old. As well as being palindromic, the central three digits form the number of the beast: 666.

Digit patterns such as 26062 displays are also useful in strengthening numeracy in young children. A simple exercise might be as follows: given the digits 0, 2, 2, 6, 6, arrange them in such a way that the resultant number reads the same from left to right. Two arrangements of course are possible: 26062 and 62026.

From the shallow waters of exercises like the previous one, it's easy to get into deep waters fairly quickly. For example, 26062 has the property that, when it is tripled and 1 is added, the result is also a palindrome: 78187. This tripling and adding one reminded me of the Collatz conjecture that I've written about in earlier posts. However, in the Collatz the rule is that for an even number like 26062, the number is halved and so, in the case of 26062, the result is 13031 (incidentally, also palindromic). I got to thinking: how would a sort of reversed Collatz sequence behave? What is I mean is explained by the following rule for a given number \(n\):

• if \(n\) is even, \(n \rightarrow 3n+1\)
• if \(n\) is odd, \( n \rightarrow \dfrac{n-1}{2} \)

Now the Collatz rule is the opposite of this and, as far as is known, always leads to 1. However, for this reversed version, I found that the sequence started to loop once it reacted 40 (going back to 121 - shown in blue). Here is the sequence:

26062, 78187, 39093, 19546, 58639, 29319, 14659, 7329, 3664, 10993, 5496, 16489, 8244, 24733, 12366, 37099, 18549, 9274, 27823, 13911, 6955, 3477, 1738, 5215, 2607, 1303, 651, 325, 162, 487, 243, 121, 60, 181, 90, 271, 135, 67, 33, 16, 49, 24, 73, 36, 109, 54, 163, 81, 40

A little experimenting showed that some numbers go to 1. For example, here is the sequence for 1000:

1000, 3001, 1500, 4501, 2250, 6751, 3375, 1687, 843, 421, 210, 631, 315, 157, 78, 235, 117, 58, 175, 87, 43, 21, 10, 31, 15, 7, 3, 1

999 on the other hand enters a different loop to that of 26062. It would be interesting to explore the different results in a future post but here I'm just illustrating how there can be complexity hiding in apparent simplicity when exploring the properties of a number.

While on the subject of 26062, it can be noted that it has the interesting property that the sum of its prime divisors is also a palindrome (242). It is in fact a member of OEIS A046354:

A046354

Composite palindromes whose sum of prime factors is palindromic (counted with multiplicity).

The sequence runs 4, 6, 8, 9, 121, 292, 444, 575, 717, 828, 989, 1331, 2002, 4884, 5445, 8668, 9559, 10201, 11211, 11811, 13231, 14241, 14541, 14641, 15251, 15751, 16261, 16761, 18281, 19291, 19591, 20002, 21112, 21312, 22022, 22922, 23832, 26062, ...

It can be generated using the following SageMath code (permalink):

P=[]

for number in [1..26062]:

    N=number.digits()

    s=""

    for n in N:

        s+=str(n)

    if number==int(s):

        P.append(number)

L=[]

for p in P:

    if is_prime(p)==0:

        sum=0

        M=list(factor(p))

        for m in M:

            sum+=m[0]*m[1]

        if sum in P:

            L.append(p)

print(L)